Recta secante, tangente o exterior a una elipse

En el plano, una recta puede comportarse de tres maneras distintas respecto a una elipse:

• Es secante si la corta en dos puntos distintos.
  
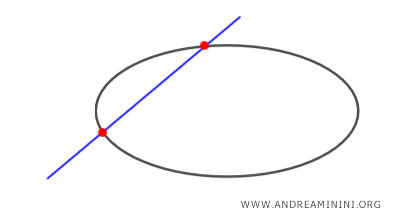
• Es tangente si la toca en un único punto.
  
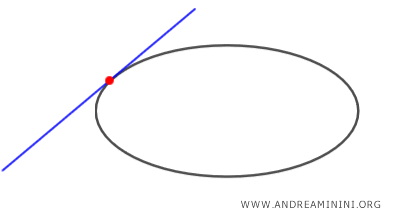
• Es exterior si no la intersecta en ningún punto.
  

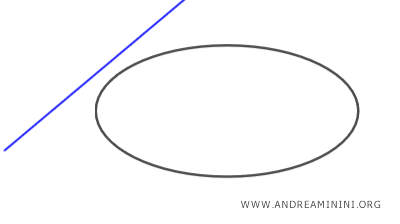
Para determinar los puntos de intersección, se resuelve el sistema formado por la ecuación de la recta y la de la elipse.

Si el sistema tiene dos soluciones reales distintas, la recta es secante. Si tiene una única solución real, es tangente. Si no presenta soluciones reales, se trata de una recta exterior.

Un ejemplo práctico

Consideremos la elipse:

$$ x^2 + 4y^2 = 40 $$

y la recta:

$$ x + 6y - 20 = 0 $$

Queremos determinar si la recta es secante, tangente o exterior respecto a la elipse.

Planteamos el sistema:

$$ \begin{cases} x^2 + 4y^2 = 40 \\ \\ x + 6y - 20 = 0 \end{cases} $$

Resolvemos por el método de sustitución:

$$ \begin{cases} x^2 + 4y^2 = 40 \\ \\ x = 20 - 6y \end{cases} $$

Sustituimos en la ecuación de la elipse:

$$ \begin{cases} (20 - 6y)^2 + 4y^2 = 40 \\ \\ x = 20 - 6y \end{cases} $$

Desarrollamos los términos:

$$ \begin{cases} 400 - 240y + 36y^2 + 4y^2 - 40 = 0 \\ \\ x = 20 - 6y \end{cases} $$

$$ \begin{cases} 40y^2 - 240y + 360 = 0 \\ \\ x = 20 - 6y \end{cases} $$

Simplificamos dividiendo la primera ecuación primero por 10 y luego por 4:

$$ \begin{cases} 4y^2 - 24y + 36 = 0 \\ \\ x = 20 - 6y \end{cases} $$

$$ \begin{cases} y^2 - 6y + 9 = 0 \\ \\ x = 20 - 6y \end{cases} $$

La ecuación cuadrática \( y^2 - 6y + 9 = 0 \) es la ecuación resolvente del sistema. Calculamos su discriminante:

$$ \Delta = b^2 - 4ac $$

$$ \Delta = (-6)^2 - 4 \cdot 1 \cdot 9 = 36 - 36 = 0 $$

Como el discriminante es cero, existe una única solución real. Por lo tanto, la recta es tangente a la elipse.

Resolvemos la ecuación para obtener el valor de \( y \):

$$ y = \frac{-b \pm \sqrt{\Delta}}{2a} $$

$$ y = \frac{-(-6) \pm \sqrt{0}}{2 \cdot 1} = \frac{6}{2} = 3 $$

Reemplazamos \( y = 3 \) en la ecuación de la recta para hallar el valor de \( x \):

$$ x = 20 - 6 \cdot 3 = 2 $$

Así, el punto de tangencia es \( (2, 3) \).

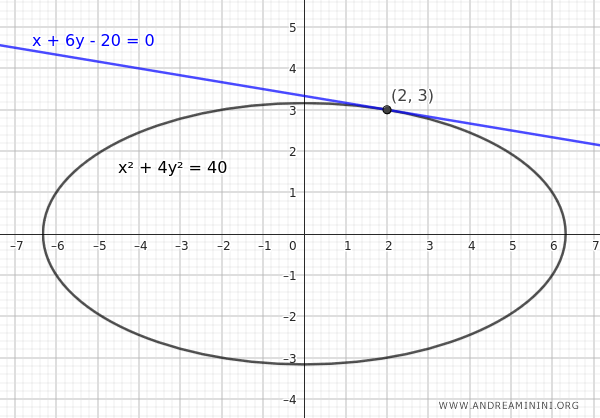
Con este procedimiento determinamos si una recta es secante, tangente o exterior a una elipse.