Ecuación de la elipse
La ecuación de la elipse en un sistema de coordenadas cartesianas centrado en el punto medio entre los focos (es decir, en el centro de la elipse) es: $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$ con $ a > 0 $ y $ b > 0 $.
Aquí, x e y son las coordenadas de un punto cualquiera \( P(x;y) \) perteneciente a la elipse.
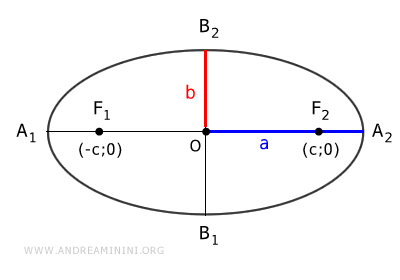
- \(a\) es el semieje mayor, que representa la distancia desde el centro hasta el extremo más alejado sobre el eje horizontal.
- \(b\) es el semieje menor, que representa la distancia desde el centro hasta el punto más cercano sobre el eje vertical.
Esta es la llamada forma canónica de la ecuación de la elipse, válida tanto si el eje mayor es horizontal como si es vertical.
Si la elipse está centrada en un punto \((h, k)\) distinto del origen, su ecuación se convierte en:
$$ \frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1 $$
En general, una elipse se define como el conjunto de puntos cuya suma de distancias a dos puntos fijos, llamados focos, permanece constante.
Nota. En la ecuación de la elipse, los coeficientes deben ser estrictamente positivos $ a > 0 $ y $ b > 0 $, ya que representan las longitudes de los semiejes. Además, el término constante debe ser positivo e igual a 1. Si es distinto de 1, puede obtenerse una ecuación equivalente dividiendo todos los términos por ese valor.
Ejes, vértices, focos y excentricidad de la elipse
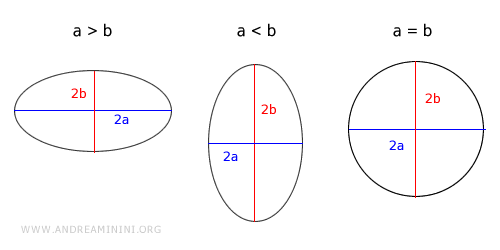
La relación entre \( a \) y \( b \) determina la orientación del eje mayor.
- Si a > b, el eje mayor es horizontal (eje x).
- Si a < b, el eje mayor es vertical (eje y).
- Si a = b, ambos ejes son iguales y la elipse se reduce a una circunferencia.
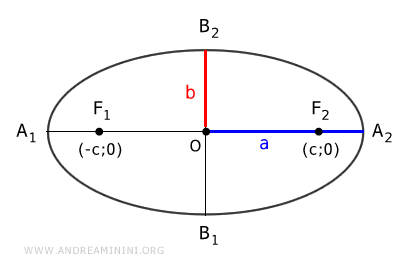
Las coordenadas de los focos dependen de la orientación del eje mayor:
- Si a > b: $$ F_1 ( - \sqrt{ a^2 - b^2 } ; 0 ) $$ $$ F_2 ( \sqrt{ a^2 - b^2 } ; 0 ) $$
- Si a < b: $$ F_1 (0; - \sqrt{ b^2 - a^2 } ) $$ $$ F_2 ( 0; \sqrt{ b^2 - a^2 } ) $$
Los valores $ \sqrt{a^2 - b^2} $ y $ \sqrt{b^2 - a^2} $ representan la semidistancia focal, es decir, la distancia entre el centro \( O \) y cada foco: $ c = \overline{OF_1} = \overline{OF_2} $.
- Si a > b: $$ c = \sqrt{a^2 - b^2} $$
- Si a < b: $$ c = \sqrt{ b^2 - a^2 } $$
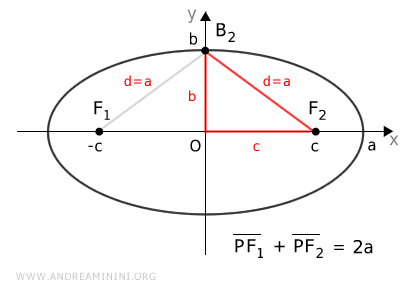
Demostración. Veamos por qué $ c = \sqrt{ a^2 - b^2 } $. En una elipse, la suma de las distancias desde cualquier punto \( P \) a los focos es constante: $$ \overline{PF_1} + \overline{PF_2} = k $$ Consideremos una elipse con eje mayor horizontal. Tomemos el punto \( A_2 \), un vértice sobre el eje mayor:
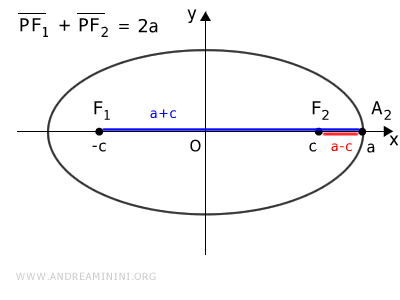
Siendo un punto de la elipse, se cumple que $$ \overline{A_2F_1} + \overline{A_2F_2} = k $$ Como $ \overline{A_2F_1} = a + c $ y $ \overline{A_2F_2} = a - c $, obtenemos: $$ (a + c) + (a - c) = k $$ $$ \require{cancel} a + \cancel{c} + a - \cancel{c} = k $$ $$ 2a = k $$ Por tanto, para cualquier punto de la elipse se cumple: $$ \overline{PF_1} + \overline{PF_2} = 2a $$ Considerando ahora el vértice \( B_2 \) sobre el eje menor:
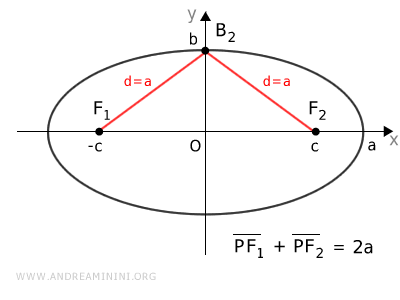
Dado que está sobre el eje de simetría, sus distancias a los focos son iguales: \( \overline{B_2F_1} = \overline{B_2F_2} \). Aplicando el teorema de Pitágoras al triángulo rectángulo \( OB_2F_2 \), se obtiene: $$ c = \sqrt{a^2 - b^2} $$
Los vértices de la elipse son los puntos de intersección con los ejes coordenados:
$$ A_1 ( -a; 0 ) $$
$$ A_2 ( a; 0 ) $$
$$ B_1 ( 0; -b ) $$
$$ B_2 ( 0; b ) $$
La excentricidad \( e \) es un parámetro que indica cuánto se desvía la elipse de ser una circunferencia. Se define como el cociente entre la distancia focal (2c) y la longitud del eje mayor (2a o 2b):
$$ e = \frac{\text{distancia focal}}{\text{longitud del eje mayor}} $$
Según la orientación de la elipse, la fórmula varía:
- Si a > b: $$ e = \frac{c}{a} = \frac{\sqrt{a^2 - b^2}}{a} = \sqrt{ 1 - \frac{b^2}{a^2} } $$
- Si a < b: $$ e = \frac{c}{b} = \frac{\sqrt{b^2 - a^2}}{b} = \sqrt{ 1 - \frac{a^2}{b^2} } $$
- Si a = b, se trata de una circunferencia y \( e = 0 \).
La excentricidad siempre cumple: $$ 0 \le e < 1 $$
Cuando \( e = 0 \), los dos focos coinciden en un solo punto y la elipse se convierte en una circunferencia perfecta.
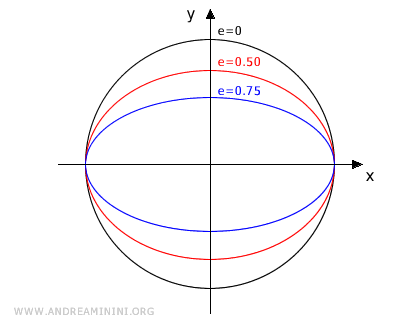
Cuanto más se acerca el valor de \( e \) a 1, más alargada es la elipse en dirección del eje mayor.
Nota. En el caso extremo \( e = 1 \), la elipse colapsa sobre el eje mayor y se denomina elipse degenerada.
Toda elipse posee dos focos y dos directrices, que son simétricas respecto al centro y perpendiculares al eje focal.
Si el eje focal es el eje \(x\), las directrices se escriben como:
$$ x = \pm \frac{a^2}{c} $$
Si el eje focal es el eje \(y\), las directrices se expresan como:
$$ y = \pm \frac{b^2}{c} $$
En general, para cualquier sección cónica, dado un punto \( P(x;y) \) sobre la elipse, el cociente entre la distancia \( \overline{PF} \) al foco y la distancia \( \overline{PH} \) a la directriz es igual a la excentricidad:
$$ e = \frac{ \overline{PF} }{ \overline{PH} } $$
Observa este ejemplo donde se ilustran las directrices de una elipse:
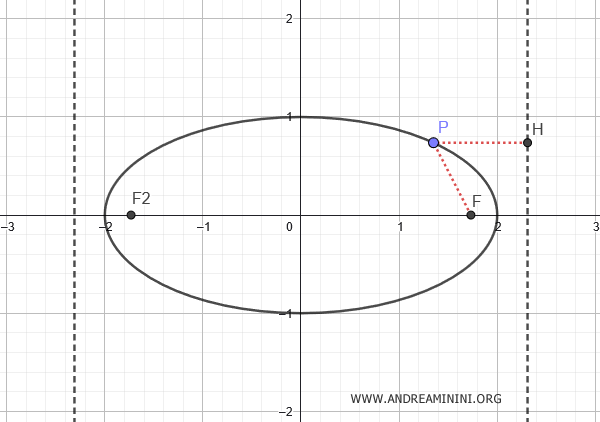
Demostración: Consideremos una elipse con eje mayor sobre el eje x: $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$ Una directriz es una recta perpendicular al eje x que pasa por el punto \( x = k \), donde \( k = \frac{a^2}{c} \). Por definición: $$ \frac{ \overline{PF} }{ \overline{PH} } = e = \frac{c}{a} $$ Tomando el punto \( A(a,0) \), se tiene \( \overline{PF} = a - c \) y \( \overline{PH} = k - a \): $$ \frac{ a-c }{ k-a } = \frac{c}{a} $$ $$ a(a - c) = c(k - a) $$ $$ \require{cancel} a^2 - \cancel{ac} = ck - \cancel{ac} $$ $$ a^2 = ck $$ $$ k = \frac{a^2}{c} $$ Por simetría, las dos directrices se encuentran en \( x = \pm \frac{a^2}{c} \).
Para encontrar las intersecciones con los ejes cartesianos, se sustituyen \( x = 0 \) y luego \( y = 0 \) en la ecuación de la elipse:
$$ \begin{cases} \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \\ \\ x = 0 \end{cases} $$
Se obtiene: \( y = \pm b \), es decir, los vértices \( B_1(0;-b) \) y \( B_2(0;b) \).
$$ \begin{cases} \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \\ \\ y = 0 \end{cases} $$
Se obtiene: \( x = \pm a \), es decir, los vértices \( A_1(-a;0) \) y \( A_2(a;0) \).
Un ejemplo práctico
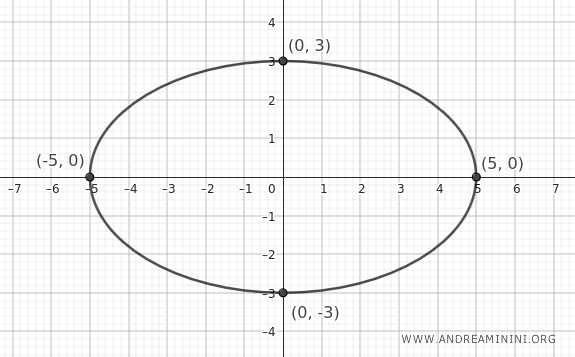
Veamos ahora una elipse cuya ecuación está expresada en su forma canónica, centrada en el origen y con los ejes principales alineados con los ejes coordenados:
$$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$
De aquí se deduce que los semiejes miden \( a = 5 \) y \( b = 3 \).
Dado que $ a > b $, el eje mayor es horizontal y coincide con el eje \( x \).
Los dos vértices principales se encuentran sobre el eje \( x \), en los puntos \( (\pm a, 0) = (\pm 5, 0) \), y los vértices secundarios están sobre el eje \( y \), en los puntos \( (0, \pm b) = (0, \pm 3) \).
- La longitud del eje mayor es la distancia entre los vértices principales: \( 2a = 2 \cdot 5 = 10 \).
- La longitud del eje menor es la distancia entre los vértices secundarios: \( 2b = 2 \cdot 3 = 6 \).
El centro de la elipse se sitúa en el origen del sistema de referencia.
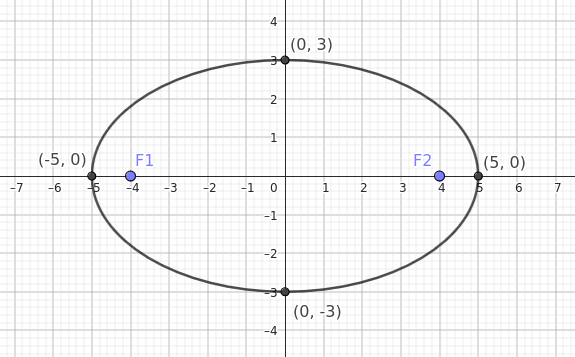
La distancia desde el centro hasta cada foco está dada por la semidistancia focal \( c \):
$$ c = \sqrt{a^2 - b^2} $$
$$ c = \sqrt{5^2 - 3^2} = \sqrt{25 - 9} = \sqrt{16} = 4 $$
Por lo tanto, los focos se ubican en \( (\pm c, 0) \), es decir, en los puntos \( (\pm 4, 0) \).
La excentricidad \( e \) de la elipse se calcula mediante la fórmula \( e = \frac{c}{a} \):
$$ e = \frac{4}{5} = 0.8 $$
El eje focal coincide con el eje \( x \), por lo que las directrices se expresan como:
$$ x = \pm \frac{a^2}{c} = \pm \frac{25}{4} \approx \pm 6.25 $$
Para cualquier punto $ P(x;y) $ sobre la elipse, el cociente entre la distancia al foco y la distancia a la directriz $$ \frac{ \overline{PF} }{ \overline{PH} } $$ permanece constante, y corresponde al valor de la excentricidad.
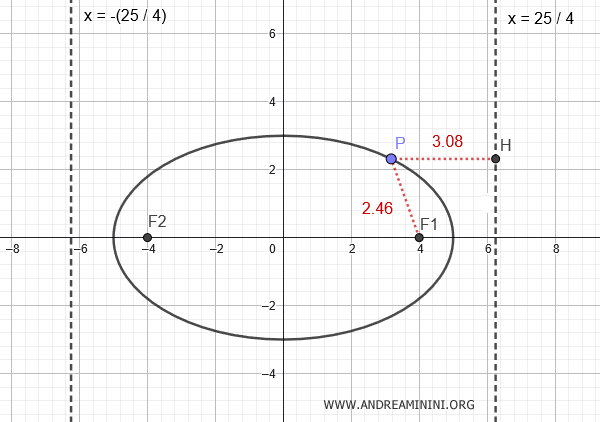
Por ejemplo, para el punto \( P \), la distancia al foco es $ \overline{PF} = 2.46 $, y la distancia a la directriz es $ \overline{PH} = 3.08 $.
El cociente entre ambas distancias es igual a la excentricidad de la elipse:
$$ \frac{ \overline{PF} }{ \overline{PH} } = \frac{2.46}{3.08} = 0.8 = e $$
Esta relación se verifica para todos los puntos de la elipse.
Con esto concluye el análisis completo de esta elipse.
Nota. Para reconocer rápidamente si una ecuación cuadrática representa una elipse, basta con examinar su forma general y analizar los coeficientes de los términos cuadráticos y el término independiente. Una ecuación representa una elipse cuando los coeficientes de los términos cuadráticos son positivos y el término independiente es positivo e igual a 1. Consideremos algunos ejemplos:
- La ecuación $ x^2 - 4y^2 = 1 $ no define una elipse, ya que uno de los términos cuadráticos es negativo.
- La ecuación $ x^2 + 4y^2 = -1 $ tampoco es válida, porque el término independiente es negativo.
- La ecuación $ 4x^2 = 4 - 2y^2 $ sí representa una elipse, ya que puede reescribirse en forma canónica: $$ 4x^2 = 4 - 2y^2 $$ $$ 4x^2 + 2y^2 = 4 $$ $$ \frac{4x^2 + 2y^2}{4} = 1 $$ $$ x^2 + \frac{y^2}{2} = 1 $$
- La ecuación $ -4x^2 - 2y^2 = -2 $ también representa una elipse, ya que: $$ (-1)(-4x^2 - 2y^2) = 2 $$ $$ 4x^2 + 2y^2 = 2 $$ $$ \frac{4x^2 + 2y^2}{2} = 1 $$ $$ 2x^2 + y^2 = 1 $$ $$ \frac{x^2}{\frac{1}{2}} + y^2 = 1 $$
Notas adicionales
Algunas observaciones complementarias sobre la ecuación de la elipse:
- La ecuación de la elipse no representa una función, ya que a cada valor de \( x \) (excepto en los extremos del eje mayor, es decir, en los puntos \( A_1 \) y \( A_2 \)) le corresponden dos valores de \( y \). A partir de la ecuación: $$ y^2 = b^2 \cdot \left(1 - \frac{x^2}{a^2} \right) $$ $$ \sqrt{y^2} = \sqrt{ \frac{b^2}{a^2} \cdot (a^2 - x^2)} $$ $$ y = \pm \frac{b^2}{a^2} \cdot \sqrt{a^2 - x^2} $$ Se puede interpretar como la unión de dos funciones: $$ y = \frac{b^2}{a^2} \cdot \sqrt{a^2 - x^2} $$ y $$ y = - \frac{b^2}{a^2} \cdot \sqrt{a^2 - x^2} $$
Y así continúa el estudio.