Cómo determinar la ecuación de una elipse a partir de su excentricidad y uno de sus vértices

Para obtener la ecuación de una elipse centrada en el origen, de la forma $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$, y conociendo uno de sus vértices $ V(x_v, y_v) $ junto con la excentricidad $ e $, es fundamental determinar si el eje mayor es horizontal o vertical.

Si el eje mayor es horizontal (a > b), se utiliza la fórmula $ e = \frac{c}{a} $ y la relación $ c^2 = a^2 - b^2 $.
Si el eje mayor es vertical (b > a), se emplea $ e = \frac{c}{b} $ junto con $ c^2 = b^2 - a^2 $.

Conocer las coordenadas del vértice permite identificar la longitud de uno de los semiejes.

Cuando el enunciado no especifica la dirección del eje mayor, es necesario analizar ambas configuraciones posibles.

Ejemplo práctico

Supongamos una elipse centrada en el origen, con un vértice en $(-3, 0)$ y excentricidad $ e = \frac{\sqrt{7}}{3} $.

Dado que sólo se proporciona un vértice, no se puede determinar directamente la orientación del eje mayor.

Por tanto, se consideran dos casos: eje mayor horizontal y eje mayor vertical.

1] Eje mayor horizontal

En este caso, el vértice se encuentra sobre el eje $x$, por lo que el semieje mayor es $ a = 3 $.

Aplicando la definición de excentricidad:

$$ e = \frac{c}{a} = \frac{\sqrt{7}}{3} $$

De donde se deduce que $ c = \sqrt{7} $.

La relación entre los semiejes en este caso es:

$$ c^2 = a^2 - b^2 $$

Reemplazando los valores conocidos:

$$ 7 = 9 - b^2 \quad \Rightarrow \quad b^2 = 2 \quad \Rightarrow \quad b = \sqrt{2} $$

Con $ a = 3 $ y $ b = \sqrt{2} $, la ecuación de la elipse resulta:

$$ \frac{x^2}{9} + \frac{y^2}{2} = 1 $$

Esta es la ecuación de la elipse con vértice en $(-3, 0)$ y excentricidad $ e = \frac{\sqrt{7}}{3} $, suponiendo eje mayor horizontal.

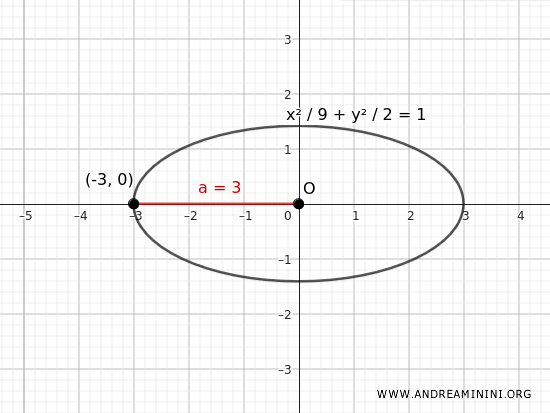
Representación gráfica de la elipse con eje mayor horizontal

Nota: Con $ a = 3 $, $ b = \sqrt{2} $ y $ c = \sqrt{7} $, se verifica: $$ e = \frac{c}{a} = \frac{\sqrt{7}}{3} $$

2] Eje mayor vertical

En este escenario, el eje mayor se encuentra en dirección vertical, y el vértice dado corresponde al semieje menor horizontal, es decir $ a = 3 $.

La excentricidad se define como $ e = \frac{c}{b} $, y la relación entre los semiejes es:

$$ c^2 = b^2 - a^2 $$

Partimos de la ecuación:

$$ \frac{\sqrt{b^2 - a^2}}{b} = \frac{\sqrt{7}}{3} $$

Sustituyendo $ a = 3 $:

$$ \frac{\sqrt{b^2 - 9}}{b} = \frac{\sqrt{7}}{3} $$

Multiplicando ambos miembros por $ b $:

$$ \sqrt{b^2 - 9} = \frac{\sqrt{7}}{3} b $$

Elevando al cuadrado:

$$ b^2 - 9 = \frac{7}{9} b^2 \quad \Rightarrow \quad \frac{2}{9} b^2 = 9 \quad \Rightarrow \quad b^2 = \frac{81}{2} $$

De donde:

$$ b = \frac{9 \sqrt{2}}{2} $$

Con $ a = 3 $ y $ b = \frac{9 \sqrt{2}}{2} $, sustituimos en la ecuación de la elipse:

$$ \frac{x^2}{9} + \frac{y^2}{\frac{81}{2}} = \frac{x^2}{9} + \frac{2 y^2}{81} = 1 $$

Esta es la ecuación de la elipse con vértice en $(-3, 0)$ y excentricidad $ e = \frac{\sqrt{7}}{3} $, si el eje mayor es vertical.

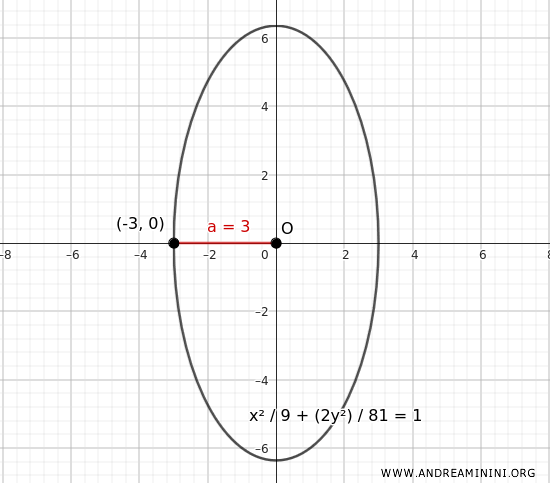
Representación gráfica de la elipse con eje mayor vertical

Nota: Con $ a = 3 $, $ b = \frac{9 \sqrt{2}}{2} $, la excentricidad se calcula como: $$ e = \frac{c}{b} = \frac{\sqrt{b^2 - a^2}}{b} = \frac{\sqrt{ \frac{81}{2} - 9 }}{ \frac{9 \sqrt{2}}{2} } = \frac{\sqrt{ \frac{63}{2} }}{ \frac{9 \sqrt{2}}{2} } $$ $$ = \frac{ \sqrt{63} }{ \sqrt{2} } \cdot \frac{2}{9 \sqrt{2} } = \frac{ 3 \sqrt{7} }{ \sqrt{2} } \cdot \frac{2}{9 \sqrt{2} } = \frac{ 3 \sqrt{14} }{9 \cdot 2} = \frac{ \sqrt{14} }{6} \quad \Rightarrow \quad e = \frac{\sqrt{7}}{3} $$

En conclusión, sin información adicional, ambas ecuaciones son soluciones válidas para la elipse descrita.

Y así sucesivamente.