Cómo determinar la ecuación de una elipse a partir de su excentricidad y uno de sus focos
Para determinar la ecuación de una elipse centrada en el origen, conociendo su excentricidad \( e = \frac{2 \sqrt{5}}{5} \) y las coordenadas de uno de sus focos, se siguen los siguientes pasos:
- La posición del foco permite identificar la dirección del eje mayor de la elipse.
- Si el eje mayor es horizontal (a > b), se aplica la fórmula $$ e = \frac{c}{a} $$. Si es vertical (a < b), se utiliza $$ e = \frac{c}{b} $$.
- La excentricidad permite calcular la longitud del semieje mayor.
- Una vez determinado el semieje mayor, se obtiene el semieje menor usando la relación \( c = \sqrt{a^2 - b^2} \) si el eje mayor es horizontal, o \( c = \sqrt{b^2 - a^2} \) si es vertical.
Ejemplo práctico
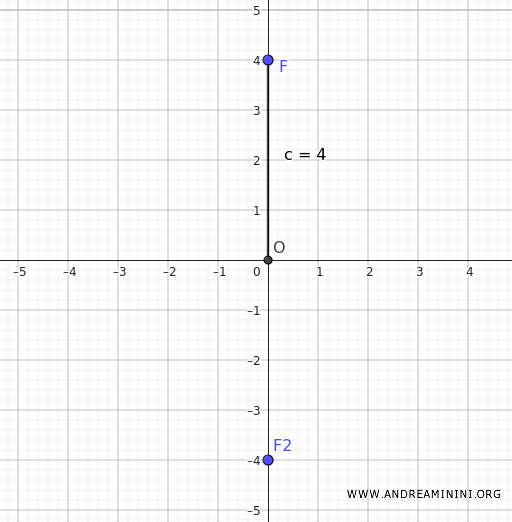
Supongamos una elipse centrada en el origen, con excentricidad \( e = \frac{2 \sqrt{5}}{5} \) y uno de sus focos en \((0, 4)\).
Dado que los focos de una elipse con centro en el origen son simétricos respecto a éste, el otro foco se encuentra en \((0, -4)\).

Como los focos siempre se ubican sobre el eje mayor, podemos concluir que en este caso dicho eje es vertical.
La distancia entre los dos focos, es decir \(2c\), corresponde a la distancia entre los puntos \((0, 4)\) y \((0, -4)\), que es igual a 8:
$$ 2c = \sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2} $$
$$ 2c = \sqrt{(0 - 0)^2 + (4 - (-4))^2} = \sqrt{8^2} = 8 $$
Por tanto, la distancia del centro a un foco es:
$$ c = 4 $$
En el caso de una elipse con eje mayor vertical, la excentricidad se define como:
$$ e = \frac{c}{b} $$
Con \(e = \frac{2 \sqrt{5}}{5}\) y \(c = 4\), despejamos el valor de \(b\):
$$ \frac{2 \sqrt{5}}{5} = \frac{4}{b} $$
$$ b = \frac{4 \cdot 5}{2 \sqrt{5}} = \frac{20}{2 \sqrt{5}} = \frac{10}{\sqrt{5}} = 2\sqrt{5} $$
Ahora calculamos el semieje menor \(a\). Para el caso de eje mayor vertical (b > a), se cumple:
$$ c = \sqrt{b^2 - a^2} $$
Sustituyendo \(b = 2\sqrt{5}\) y \(c = 4\):
$$ 4 = \sqrt{(2\sqrt{5})^2 - a^2} = \sqrt{4 \cdot 5 - a^2} = \sqrt{20 - a^2} $$
Elevando al cuadrado ambos miembros:
$$ 16 = 20 - a^2 \quad \Rightarrow \quad a^2 = 4 \quad \Rightarrow \quad a = 2 $$
Por lo tanto, el semieje menor horizontal mide 2 unidades.
Con \(a = 2\) y \(b = 2\sqrt{5}\), la ecuación de la elipse resulta ser:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{4} + \frac{y^2}{20} = 1 $$
Esta es la ecuación buscada:
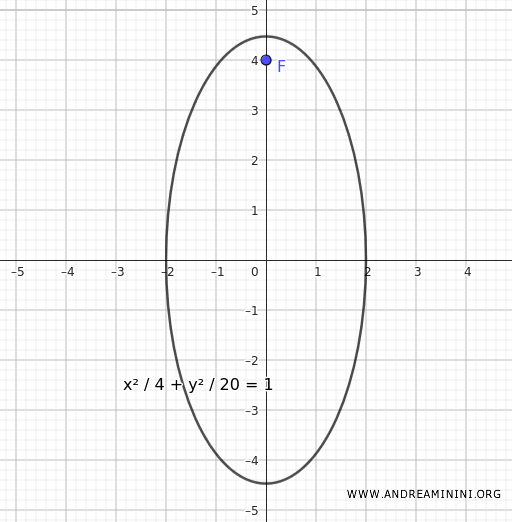
$$ \frac{x^2}{4} + \frac{y^2}{20} = 1 $$
Representación gráfica:
Y así sucesivamente.