Cómo determinar la ecuación de una elipse a partir de un punto y la excentricidad

Para encontrar la ecuación de una elipse centrada en el origen, conociendo las coordenadas de un punto por el que pasa y su excentricidad, se sustituyen dichas coordenadas en la ecuación general:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

Según si el eje mayor es horizontal o vertical, se utiliza la fórmula correspondiente para la excentricidad:

• Si el eje mayor es horizontal (a > b): $$ e = \sqrt{1 - \frac{b^2}{a^2} } $$
• Si el eje mayor es vertical (b > a): $$ e = \sqrt{1 - \frac{a^2}{b^2} } $$

Se plantea un sistema de ecuaciones con estas condiciones y se resuelven las variables desconocidas.

Nota: Si no se sabe cuál es el eje mayor, hay que analizar ambos casos posibles.

Ejemplo práctico

Supongamos que una elipse pasa por el punto \((1, -\sqrt{3})\) y tiene una excentricidad \( e = \frac{\sqrt{3}}{3} \).

Como desconocemos la dirección del eje mayor, analizaremos ambas opciones.

1] Primer caso: \(a\) es el eje mayor (a > b)

Si el eje mayor es horizontal, la fórmula de la excentricidad es:

$$ e = \sqrt{1 - \frac{b^2}{a^2}} = \frac{\sqrt{3}}{3} $$

Elevamos ambos lados al cuadrado:

$$ \left( \sqrt{1 - \frac{b^2}{a^2}} \right)^2 = \left( \frac{\sqrt{3}}{3} \right)^2 $$

$$ 1 - \frac{b^2}{a^2} = \frac{1}{3} $$

$$ \frac{b^2}{a^2} = 1 - \frac{1}{3} = \frac{2}{3} $$

De aquí se obtiene:

$$ b^2 = \frac{2}{3} a^2 \quad \Rightarrow \quad b = a \sqrt{\frac{2}{3}} $$

Sustituimos el punto \((1, -\sqrt{3})\) en la ecuación general:

$$ \frac{1^2}{a^2} + \frac{(-\sqrt{3})^2}{b^2} = 1 $$

Como \( b = a \sqrt{\frac{2}{3}} \), reemplazamos en la expresión:

$$ \frac{1}{a^2} + \frac{3}{(a \cdot \sqrt{ \frac{2}{3} })^2} = 1 $$

$$ \frac{1}{a^2} + \frac{3}{a^2 \cdot \frac{2}{3}} = 1 $$

$$ \frac{1}{a^2} + \frac{9}{2a^2} = 1 $$

$$ \frac{11}{2a^2} = 1 \quad \Rightarrow \quad a^2 = \frac{11}{2} \quad \Rightarrow \quad a = \sqrt{\frac{11}{2}} $$

Calculamos \( b \):

$$ b = a \sqrt{\frac{2}{3}} = \sqrt{\frac{11}{2}} \cdot \sqrt{\frac{2}{3}} = \sqrt{\frac{11}{3}} $$

La ecuación de la elipse queda entonces:

$$ \frac{x^2}{ \frac{11}{2} } + \frac{y^2}{ \frac{11}{3} } = 1 \quad \Rightarrow \quad \frac{2x^2}{11} + \frac{3y^2}{11} = 1 $$

Representación gráfica:

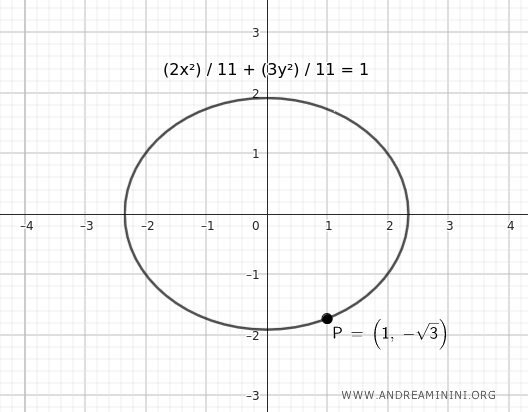
La elipse pasa por el punto indicado.

2] Segundo caso: \(a\) es el eje menor (a < b)

Cuando el eje mayor es vertical, se usa la fórmula:

$$ e = \sqrt{1 - \frac{a^2}{b^2}} = \frac{\sqrt{3}}{3} $$

Elevando ambos lados al cuadrado:

$$ 1 - \frac{a^2}{b^2} = \frac{1}{3} \quad \Rightarrow \quad \frac{a^2}{b^2} = \frac{2}{3} $$

De aquí se obtiene:

$$ a = b \sqrt{\frac{2}{3}} $$

Sustituimos el punto en la ecuación general:

$$ \frac{1^2}{a^2} + \frac{(-\sqrt{3})^2}{b^2} = 1 $$

Reemplazando \( a = b \sqrt{\frac{2}{3}} \):

$$ \frac{1}{b^2 \cdot \frac{2}{3}} + \frac{3}{b^2} = 1 $$

$$ \frac{3}{2b^2} + \frac{3}{b^2} = 1 \quad \Rightarrow \quad \frac{9}{2b^2} = 1 $$

$$ b^2 = \frac{9}{2} \quad \Rightarrow \quad b = \frac{3 \sqrt{2}}{2} $$

Ahora calculamos \( a \):

$$ a = \frac{3 \sqrt{2}}{2} \cdot \sqrt{\frac{2}{3}} = \frac{3}{\sqrt{3}} = \sqrt{3} $$

La ecuación de la elipse se convierte en:

$$ \frac{x^2}{3} + \frac{y^2}{\frac{9}{2}} = 1 \quad \Rightarrow \quad \frac{x^2}{3} + \frac{2y^2}{9} = 1 $$

Representación gráfica correspondiente:

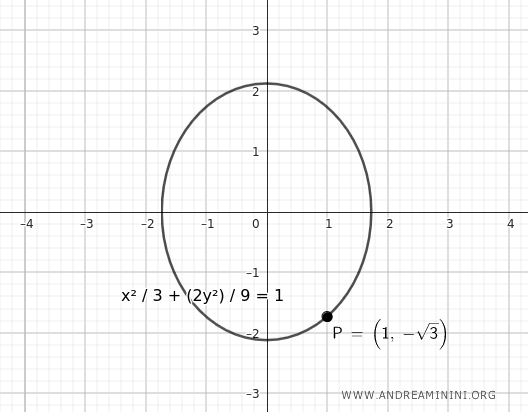
Por tanto, la elipse que pasa por el punto \((1, -\sqrt{3})\) y tiene una excentricidad \( \frac{\sqrt{3}}{3} \), puede describirse mediante cualquiera de estas dos ecuaciones, dependiendo de cuál sea el eje mayor.

Y así sucesivamente.