Cómo determinar la ecuación de una elipse a partir de dos puntos conocidos
Para encontrar la ecuación de una elipse centrada en el origen que pasa por dos puntos dados \( (x_1, y_1) \) y \( (x_2, y_2) \), basta sustituir sus coordenadas en la forma general de la elipse, lo que conduce a un sistema de dos ecuaciones con dos incógnitas:
$$ \begin{cases} \frac{x_1^2}{a^2} + \frac{y_1^2}{b^2} = 1 \\ \\ \frac{x_2^2}{a^2} + \frac{y_2^2}{b^2} = 1 \end{cases} $$
Resolver este sistema nos permite determinar las longitudes de los semiejes \(a\) y \(b\).
Ejemplo práctico
Buscamos la ecuación de la elipse centrada en el origen que pasa por los puntos \( A \left( \sqrt{3}, \frac{1}{2} \right) \) y \( B \left( -1, \frac{\sqrt{3}}{2} \right) \).
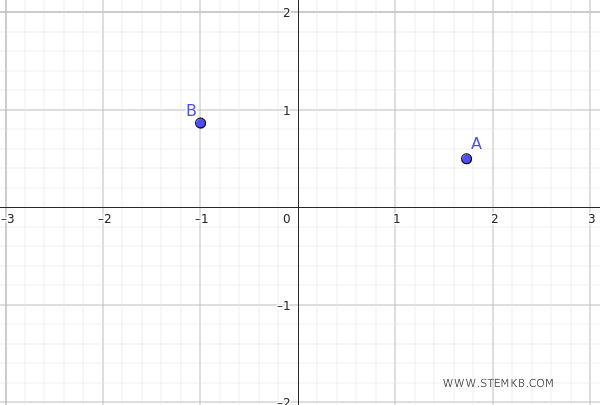
Partimos de la forma canónica de la elipse con ejes alineados con los ejes cartesianos:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
donde \(a\) y \(b\) representan las longitudes de los semiejes horizontal y vertical, respectivamente.
Sustituimos las coordenadas de los puntos conocidos para obtener dos ecuaciones.
Para el punto \( A \left( \sqrt{3}, \frac{1}{2} \right) \):
$$ \frac{3}{a^2} + \frac{1}{4b^2} = 1 $$
Para el punto \( B \left( -1, \frac{\sqrt{3}}{2} \right) \):
$$ \frac{1}{a^2} + \frac{3}{4b^2} = 1 $$
Así obtenemos el sistema:
$$ \begin{cases} \frac{3}{a^2} + \frac{1}{4b^2} = 1 \\ \\ \frac{1}{a^2} + \frac{3}{4b^2} = 1 \end{cases} $$
Multiplicamos la primera ecuación por 3 para poder eliminar el término con \( \frac{1}{4b^2} \):
$$ \begin{cases} \frac{9}{a^2} + \frac{3}{4b^2} = 3 \\ \\ \frac{1}{a^2} + \frac{3}{4b^2} = 1 \end{cases} $$
Restando miembro a miembro:
$$ \left( \frac{9}{a^2} + \frac{3}{4b^2} \right) - \left( \frac{1}{a^2} + \frac{3}{4b^2} \right) = 2 $$
$$ \frac{8}{a^2} = 2 \quad \Rightarrow \quad a^2 = 4 \quad \Rightarrow \quad a = 2 $$
Ahora sustituimos \( a^2 = 4 \) en una de las ecuaciones originales para hallar \( b^2 \):
$$ \frac{1}{4} + \frac{3}{4b^2} = 1 \quad \Rightarrow \quad \frac{3}{4b^2} = \frac{3}{4} \quad \Rightarrow \quad b^2 = 1 \quad \Rightarrow \quad b = 1 $$
Hemos obtenido los valores de ambos semiejes: \( a = 2 \), \( b = 1 \).
Por tanto, la ecuación de la elipse es:
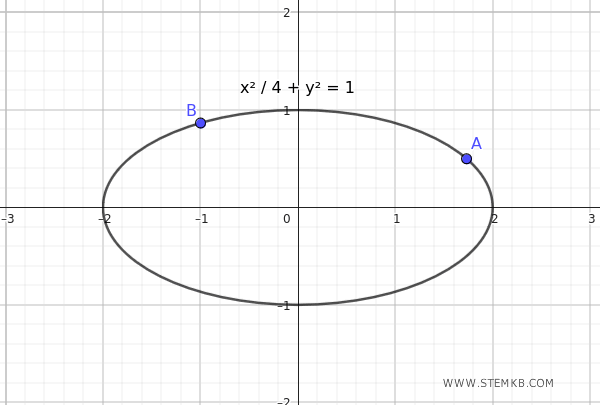
$$ \frac{x^2}{4} + y^2 = 1 $$
Esta elipse pasa por los puntos \( A \left( \sqrt{3}, \frac{1}{2} \right) \) y \( B \left( -1, \frac{\sqrt{3}}{2} \right) \), tal como se requería.
Y con eso, concluimos.