Cómo determinar la ecuación de una elipse a partir de sus semiejes

Cuando se conocen las longitudes de los semiejes de una elipse, es posible obtener su ecuación de forma inmediata. Existen dos situaciones principales que conviene distinguir:

• Elipse con centro en el origen (0, 0)
  Si la elipse está centrada en el origen del sistema de coordenadas cartesianas, su ecuación se expresa directamente en función de \(a\), la longitud del semieje horizontal, y \(b\), la del semieje vertical: $$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
• Elipse con centro en un punto \((h, k)\)
  Si el centro de la elipse se encuentra en un punto \( P(h,k) \), su ecuación general es: $$ \frac{(x - h)^2}{a^2} + \frac{(y - k)^2}{b^2} = 1 $$ donde \(a\) y \(b\) representan, respectivamente, las longitudes de los semiejes horizontal y vertical.

Ejemplo

Supongamos una elipse centrada en el origen, con semieje horizontal \(a = 5\) y semieje vertical \(b = 3\).

Su ecuación será:

$$ \frac{x^2}{5^2} + \frac{y^2}{3^2} = 1 $$

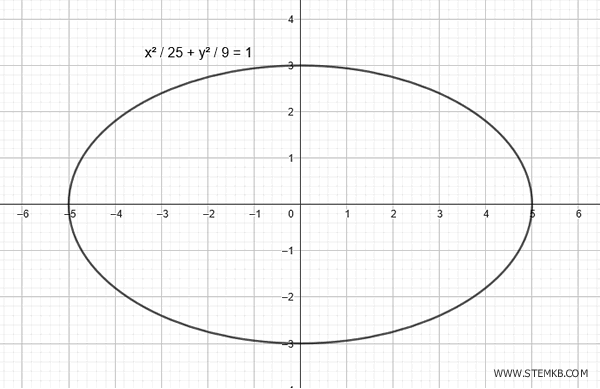
$$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$

A continuación se muestra el gráfico de esta elipse:

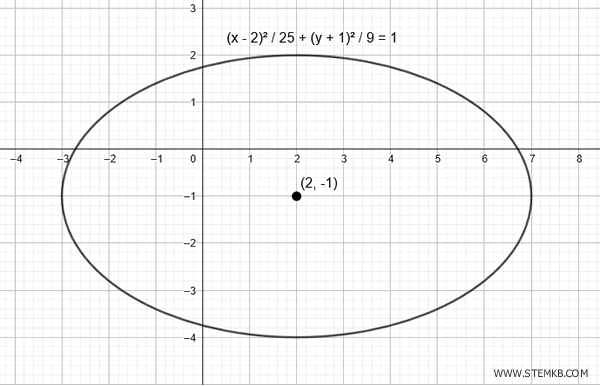
Si trasladamos el centro de la elipse al punto \((2, -1)\), manteniendo los mismos semiejes, la ecuación se convierte en:

$$ \frac{(x - 2)^2}{25} + \frac{(y + 1)^2}{9} = 1 $$

El gráfico correspondiente a esta elipse trasladada es el siguiente:

Estas fórmulas generales son válidas para cualquier elipse, siempre que se conozcan las longitudes de sus semiejes y la ubicación de su centro.

Y así sucesivamente.