Cómo obtener la ecuación de una elipse a partir de un vértice y un punto

Cuando una elipse está centrada en el origen y se conocen las coordenadas de uno de sus vértices y de un punto por el que pasa, es posible determinar su ecuación sustituyendo los datos en la expresión general: $$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

Ejemplo práctico

Estudiemos una elipse con centro en el origen $ O(0,0) $, vértice en $ V(-3,0) $, que pasa por el punto $ P \left( - \frac{3\sqrt{2}}{2},\ -2 \right) $.

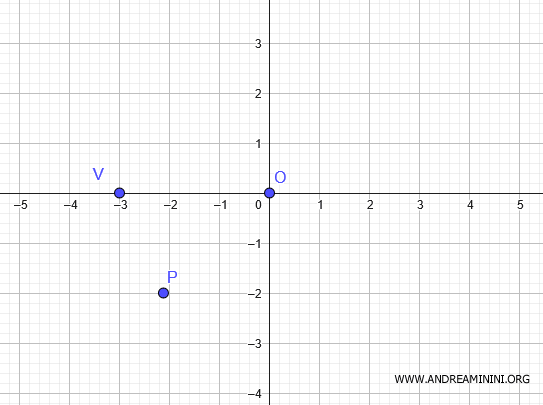
datos iniciales del problema

Como el vértice $ V(-3,0) $ se encuentra sobre el eje $ x $, el eje mayor de la elipse es horizontal.

Dado que los vértices son simétricos respecto al origen, el otro se ubica en $ V(3,0) $.

La distancia entre el vértice $ V(-3,0) $ y el origen corresponde a la longitud del semieje mayor:

$$ a = \sqrt{(x_v - x_o)^2 + (y_v - y_o)^2} = \sqrt{(-3)^2} = 3 $$

Con este dato, podemos comenzar a construir la ecuación de la elipse:

$$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

Al sustituir $ a = 3 $, obtenemos:

$$\frac{x^2}{9} + \frac{y^2}{b^2} = 1 $$

Para encontrar el valor de $ b $, usamos las coordenadas del punto $ P \left( - \frac{3\sqrt{2}}{2},\ -2 \right) $:

$$\frac{\left( - \frac{3\sqrt{2}}{2} \right)^2}{9} + \frac{(-2)^2}{b^2} = 1 $$

$$\frac{ \frac{18}{4} }{9} + \frac{4}{b^2} = 1 \quad \Rightarrow \quad \frac{9}{2 \cdot 9} + \frac{4}{b^2} = 1 $$

$$ \frac{1}{2} + \frac{4}{b^2} = 1 $$

Despejamos $ b^2 $:

$$ \frac{4}{b^2} = \frac{1}{2} \quad \Rightarrow \quad b^2 = 8 $$

$$ b = \sqrt{8} = 2\sqrt{2} $$

Ya que $ a > b $, se confirma que el eje mayor es horizontal.

Con $ a = 3 $ y $ b = 2\sqrt{2} $, sustituimos en la ecuación general:

$$\frac{x^2}{9} + \frac{y^2}{(2\sqrt{2})^2} = \frac{x^2}{9} + \frac{y^2}{8} = 1 $$

Multiplicamos ambos miembros por 72 para obtener la forma reducida:

$$ \frac{8x^2 + 9y^2}{72} = 1 \quad \Rightarrow \quad 8x^2 + 9y^2 = 72 $$

Hemos determinado la ecuación de la elipse con centro en $ O(0,0) $, vértice en $ V(-3,0) $, que pasa por el punto $ P \left( - \frac{3\sqrt{2}}{2},\ -2 \right) $.

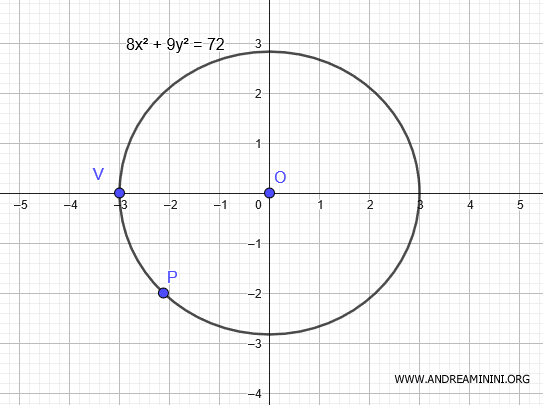
gráfico de la elipse

Así se obtiene, paso a paso, la ecuación de una elipse a partir de datos geométricos concretos.