Cómo obtener la ecuación de una elipse a partir de un foco y un vértice
Si conocemos un foco y un vértice de una elipse centrada en el origen, podemos determinar su ecuación calculando la longitud del semieje restante mediante el teorema de Pitágoras.
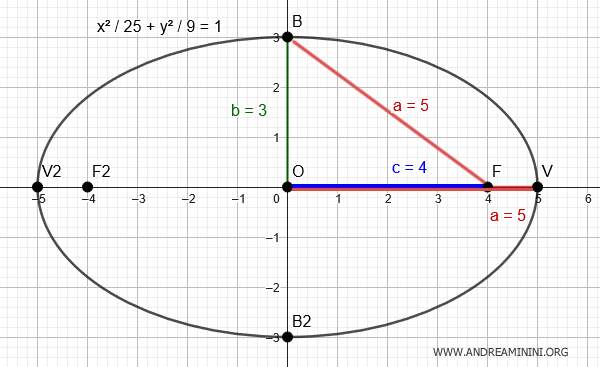
La configuración geométrica forma un triángulo cuyos vértices son el origen, un foco y un vértice (OF2B2).
En dicho triángulo, uno de los catetos \( c \) representa la distancia del foco al centro, el otro cateto \( b \) corresponde al semieje menor, y la hipotenusa \( d = a \) coincide con el semieje mayor de la elipse.
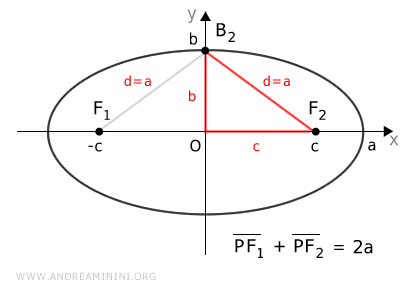
Por lo tanto, para hallar la longitud del semieje menor basta con aplicar el teorema de Pitágoras.
Nota: Es imprescindible conocer la posición del centro para poder resolver el ejercicio. Disponer únicamente de las coordenadas de un foco y un vértice no es suficiente. En este ejemplo, asumimos que la elipse está centrada en el origen \( O(0,0) \).
Un ejemplo práctico
Consideremos una elipse con centro en el origen \((0,0)\), vértice en \( V(5,0) \) y foco en \( F(4,0) \).
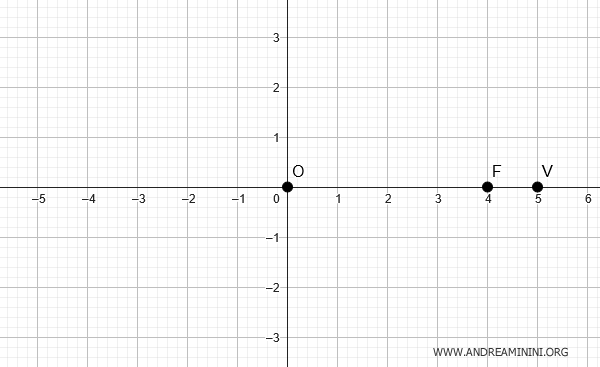
Queremos determinar su ecuación.
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
Aquí, \( a \) es la longitud del semieje mayor (eje \( x \)) y \( b \) la del semieje menor (eje \( y \)).
Como tanto el foco \( F(4,0) \) como el vértice \( V(5,0) \) se encuentran sobre el eje \( x \), el eje mayor de la elipse es horizontal.
La longitud de \( a \) corresponde a la distancia entre el centro \((0,0)\) y el vértice \( V(5,0) \):
$$ a = \sqrt{(x_v - x_o)^2 + (y_v - y_o)^2} $$
$$ a = \sqrt{(5 - 0)^2 + (0 - 0)^2} $$
$$ a = \sqrt{25} = 5 $$
Por tanto, el semieje mayor mide \( a = 5 \).
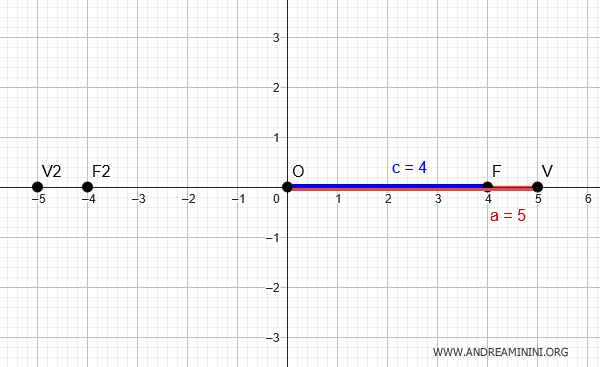
Además, la distancia del centro a uno de los focos es \( c = 4 \).
Nota: Si uno de los focos está en \((4,0)\), su simétrico se encuentra en \((-4,0)\). Del mismo modo, si un vértice está en \((5,0)\), el otro estará en \((-5,0)\), ya que ambos elementos son simétricos respecto al origen.
Conociendo los valores de \( a \) y \( c \), aplicamos el teorema de Pitágoras para calcular \( b \):
$$ c^2 = a^2 - b^2 $$
Sustituyendo los valores conocidos:
$$ 4^2 = 5^2 - b^2 $$
$$ 16 = 25 - b^2 $$
$$ b^2 = 25 - 16 = 9 $$
$$ b = 3 $$
Así, el semieje menor mide \( b = 3 \), y los extremos del eje menor se ubican en \( B(0,3) \) y \( B_2(0,-3) \).
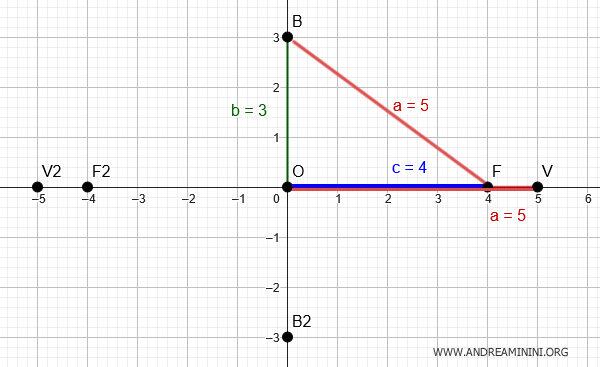
Ya contamos con todos los datos necesarios para escribir la ecuación de la elipse:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{x^2}{25} + \frac{y^2}{9} = 1 $$
Esta es la representación gráfica de dicha ecuación:
¡Y con esto, el ejercicio queda resuelto!