Método de completar el cuadrado para una elipse
El método de completar el cuadrado permite obtener las características geométricas de una elipse a partir de su ecuación general: $$ Ax^2 + By^2 + Cx + Dy + E = 0 $$ Agrupando los términos en \(x\) y en \(y\), es posible reescribir la expresión como suma de binomios al cuadrado, lo que conduce a la forma canónica de la elipse: $$ \frac{(x - x_0)^2}{a^2} + \frac{(y - y_0)^2}{b^2} = 1 $$ donde \( (x_0, y_0) \) representa el centro de la curva.
Ejemplo práctico
Consideremos la siguiente ecuación general:
$$ 25x^2 + 9y^2 - 100x - 18y - 116 = 0 $$
El objetivo es transformarla en su forma estándar: $$ \frac{(x - x_0)^2}{a^2} + \frac{(y - y_0)^2}{b^2} = 1 $$. Para ello, primero trasladamos el término constante al segundo miembro:
$$ 25x^2 + 9y^2 - 100x - 18y = 116 $$
Agrupamos los términos con \(x\) y con \(y\):
$$ 25(x^2 - 4x) + 9(y^2 - 2y) = 116 $$
Ahora completamos el cuadrado en ambos paréntesis. Para los términos en \(x\), sumamos \(4 \cdot 25\) a ambos lados:
$$ 25(x^2 - 4x + 4) + 9(y^2 - 2y) = 116 + 100 $$
$$ 25(x - 2)^2 + 9(y^2 - 2y) = 216 $$
Procedemos igual con los términos en \(y\), sumando \(1 \cdot 9\) a ambos lados:
$$ 25(x - 2)^2 + 9(y^2 - 2y + 1) = 216 + 9 $$
$$ 25(x - 2)^2 + 9(y - 1)^2 = 225 $$
Dividimos ahora entre 225 para obtener la forma reducida:
$$ \frac{25(x - 2)^2}{225} + \frac{9(y - 1)^2}{225} = 1 $$
$$ \frac{(x - 2)^2}{9} + \frac{(y - 1)^2}{25} = 1 $$
Esta es la forma canónica de la elipse.
Se deduce de inmediato que el centro está en el punto \( (2, 1) \).
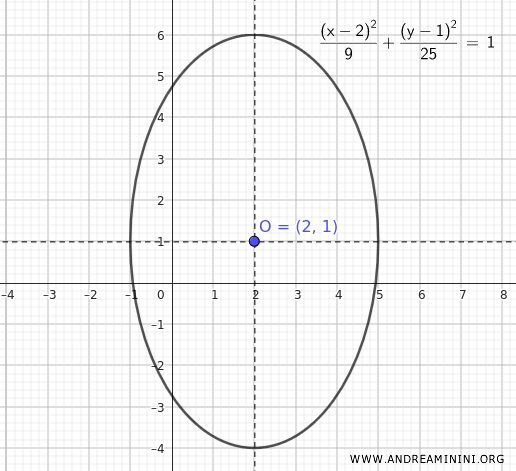
Los ejes de simetría de la elipse son las rectas \( x = 2 \) y \( y = 1 \).
Los valores \( a^2 = 9 \) y \( b^2 = 25 \) indican que los semiejes miden \( a = 3 \) y \( b = 5 \).
Como \( b > a \), el eje mayor es vertical, es decir, paralelo al eje \(y\).
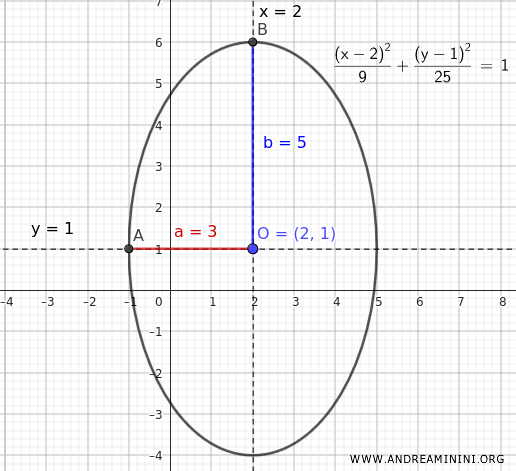
Conociendo el centro y los semiejes, podemos determinar fácilmente los vértices:
$$ A = (2 \pm a, 1) = (2 \pm 3, 1) = \begin{cases} A_1 = (-1, 1) \\ \\ A_2 = (5, 1) \end{cases} $$
$$ B = (2, 1 \pm b) = (2, 1 \pm 5) = \begin{cases} B_1 = (2, -4) \\ \\ B_2 = (2, 6) \end{cases} $$
Finalmente, podemos calcular la distancia focal utilizando la relación \( c^2 = b^2 - a^2 \):
$$ c^2 = b^2 - a^2 = 25 - 9 = 16 $$
$$ c = \sqrt{16} = 4 $$
Los focos se ubican entonces sobre el eje mayor, en los puntos:
$$ F = (2, 1 \pm 4) = \begin{cases} F_1 = (2, -3) \\ \\ F_2 = (2, 5) \end{cases} $$
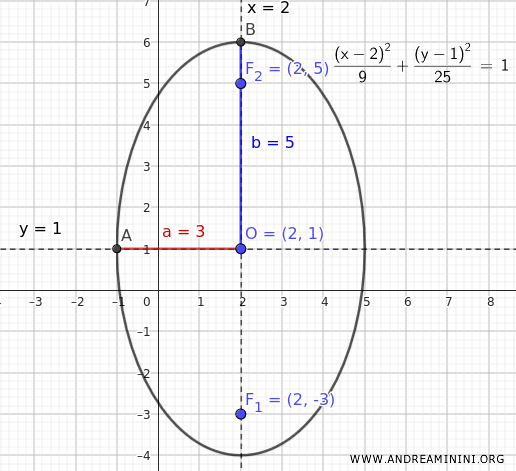
Con esto, la elipse queda completamente caracterizada.