Rectas tangentes a una elipse que pasan por un punto P
Dada una elipse y un punto cualquiera \( P \) del plano, pueden existir dos, una o ninguna recta tangente a la elipse que pase por dicho punto.
- Si el punto \( P \) está fuera de la elipse, existen exactamente dos rectas tangentes que lo atraviesan.
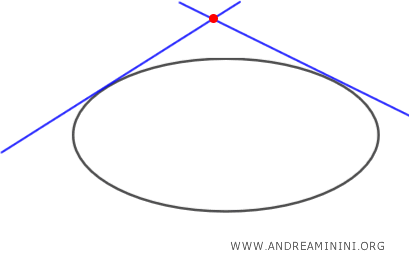
- Si \( P \) pertenece a la elipse, solo hay una recta tangente que pasa por él.
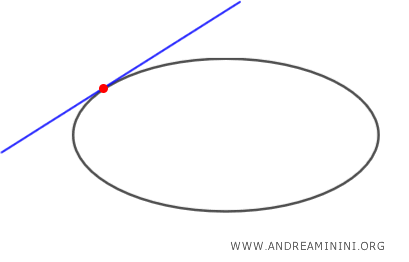
- Si \( P \) se encuentra en el interior de la elipse, no hay ninguna recta tangente que lo atraviese.
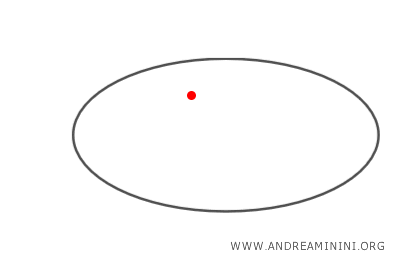
Cómo determinar las rectas tangentes a la elipse
Para hallar las ecuaciones de las rectas tangentes a una elipse que pasan por un punto \( P(x0, y0) \), comenzamos escribiendo la ecuación general de la familia de rectas que pasan por \( P \):
$$ y - y_0 = m(x - x_0) $$
Consideramos también la ecuación de la elipse:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
El objetivo es encontrar los valores de \( m \) para los cuales la recta es tangente a la elipse, es decir, toca la curva en un único punto.
Planteamos el sistema de ecuaciones:
$$ \begin{cases} y - y_0 = m(x - x_0) \\ \\ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \end{cases} $$
La condición de tangencia se traduce en que el sistema tenga una única solución real, lo cual ocurre cuando el discriminante de la ecuación resultante es nulo:
$$ \Delta = b^2 - 4ac = 0 $$
Esta condición nos permite determinar los posibles valores de \( m \). Una vez obtenidos, los sustituimos en la ecuación de la recta para obtener las rectas tangentes buscadas.
Ejemplo práctico
Sea el punto \( P(4, 4) \) y la elipse:
$$ x^2 + 4y^2 = 20 $$
Queremos saber si existen rectas tangentes a la elipse que pasen por \( P(4, 4) \), y en caso afirmativo, hallar sus ecuaciones.
Planteamos el sistema:
$$ \begin{cases} x^2 + 4y^2 = 20 \\ \\ y - 4 = m(x - 4) \end{cases} $$
Despejamos \( y \) y lo sustituimos en la ecuación de la elipse:
$$ x^2 + 4[m(x - 4) + 4]^2 = 20 $$
Desarrollamos la expresión:
$$ x^2 + 4[m^2(x - 4)^2 + 8m(x - 4) + 16] = 20 $$
$$ x^2 + 4m^2(x^2 - 8x + 16) + 32m(x - 4) + 64 = 20 $$
$$ x^2 + 4m^2x^2 - 32m^2x + 64m^2 + 32mx - 128m + 64 = 20 $$
Reuniendo los términos semejantes:
$$ x^2(1 + 4m^2) + x(-32m^2 + 32m) + (64m^2 - 128m + 44) = 0 $$
Para que esta ecuación tenga una única solución real, imponemos:
$$ \Delta = b^2 - 4ac = 0 $$
Donde:
$$ a = 1 + 4m^2, \quad b = -32m^2 + 32m, \quad c = 64m^2 - 128m + 44 $$
Calculamos el discriminante:
$$ \Delta = (-32m^2 + 32m)^2 - 4(1 + 4m^2)(64m^2 - 128m + 44) = 0 $$
Desarrollando:
$$ \Delta = 1024m^4 - 2048m^3 + 1024m^2 - 1024m^4 + 2048m^3 - 960m^2 + 512m - 176 = 0 $$
$$ \Delta = 64m^2 + 512m - 176 = 0 $$
Resolvemos esta ecuación cuadrática en \( m \) utilizando la fórmula general:
$$ m = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
con \( a = 64 \), \( b = 512 \), \( c = -176 \):
$$ m = \frac{-512 \pm \sqrt{512^2 - 4 \cdot 64 \cdot (-176)}}{128} $$
$$ m = \frac{-512 \pm \sqrt{262144 + 45056}}{128} $$
$$ m = \frac{-512 \pm \sqrt{307200}}{128} $$
$$ m = \frac{-512 \pm 554.256}{128} $$
Calculamos los valores aproximados:
$$ m_1 \approx \frac{42.256}{128} \approx 0.33 $$
$$ m_2 \approx \frac{-1066.256}{128} \approx -8.33 $$
Por tanto, las pendientes de las rectas tangentes son aproximadamente:
$$ m \approx 0.33 \quad \text{y} \quad m \approx -8.33 $$
Finalmente, sustituimos en la ecuación de la recta para obtener las tangentes:
- Para \( m \approx 0.33 \): \( y = 0.33x - 1.32 + 4 \)
- Para \( m \approx -8.33 \): \( y = -8.33x + 33.32 + 4 \)
Ambas rectas son tangentes a la elipse y pasan por el punto \( P(4, 4) \).
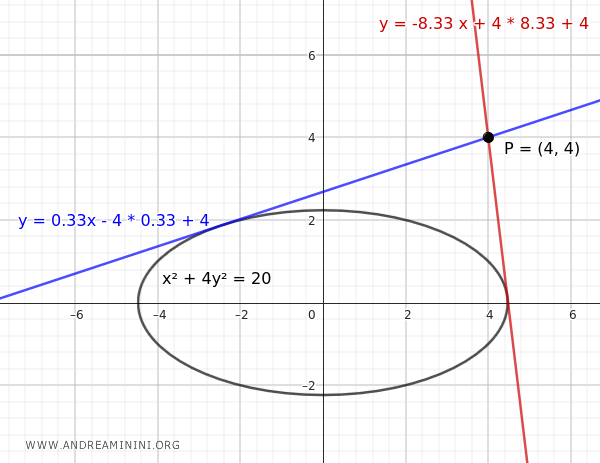
Con esto, concluimos el procedimiento.