Cómo determinar la ecuación de una elipse conociendo un foco y un punto

Si una elipse está centrada en el origen y se conocen las coordenadas de uno de sus focos $ F(c, 0) $ o $ F(0, c) $, junto con un punto $ P(x, y) $ que pertenece a ella, podemos determinar su ecuación planteando un sistema de ecuaciones para hallar los valores exactos de $ a $ y $ b $, longitudes de los semiejes.

La primera ecuación se obtiene sustituyendo las coordenadas del punto $ P(x, y) $ en la forma canónica de la elipse:

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

La segunda depende de la orientación del eje mayor, que se deduce de la posición del foco:

Si el eje mayor es horizontal: $$ c = \sqrt{a^2 - b^2} $$
Si el eje mayor es vertical: $$ c = \sqrt{b^2 - a^2} $$

Al resolver este sistema obtenemos los valores de $ a $ y $ b $, lo que nos permite escribir la ecuación completa de la elipse.

¿Cómo identificar el eje mayor? Si el foco está en $ (c, 0) $, el eje mayor es horizontal (eje $ x $); si se encuentra en $ (0, c) $, el eje mayor es vertical (eje $ y $).

Ejemplo práctico

Queremos determinar la ecuación de una elipse centrada en el origen, con un foco en $ F(0, 2 \sqrt{2}) $, que pasa por el punto $ P\left( \frac{ \sqrt{5} }{3},\ 2 \right) $.

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$

Como el foco se encuentra sobre el eje $ y $, el eje mayor es vertical.

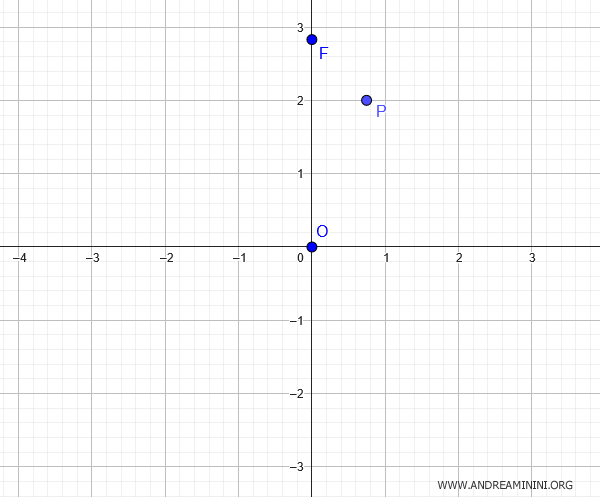
coordenadas del punto

En este caso, la relación entre los semiejes viene dada por:

$$ c = \sqrt{b^2 - a^2} $$

Como el valor del foco es $ c = 2 \sqrt{2} $, se tiene:

$$ 2 \sqrt{2} = \sqrt{b^2 - a^2} $$

Elevando ambos miembros al cuadrado:

$$ 8 = b^2 - a^2 $$

Esta es la primera ecuación del sistema.

La segunda se obtiene sustituyendo las coordenadas del punto $ P $ en la ecuación de la elipse:

$$ \frac{\left( \frac{ \sqrt{5} }{3} \right)^2}{a^2} + \frac{2^2}{b^2} = 1 $$

$$ \frac{5}{9a^2} + \frac{4}{b^2} = 1 $$

Así, el sistema queda:

$$ \begin{cases} b^2 - a^2 = 8 \\ \\ \frac{5}{9a^2} + \frac{4}{b^2} = 1 \end{cases} $$

Sustituyendo $ b^2 = 8 + a^2 $ en la segunda ecuación:

$$ \frac{5}{9a^2} + \frac{4}{8 + a^2} = 1 $$

Multiplicamos ambos miembros por $ 9a^2(8 + a^2) $ para eliminar los denominadores:

$$ 5(8 + a^2) + 4 \cdot 9a^2 - 9a^2(8 + a^2) = 0 $$

$$ 40 + 5a^2 + 36a^2 - 72a^2 - 9a^4 = 0 $$

$$ -9a^4 - 31a^2 + 40 = 0 $$

Reordenando términos:

$$ 9a^4 + 31a^2 - 40 = 0 $$

Hacemos el cambio $ k = a^2 $:

$$ 9k^2 + 31k - 40 = 0 $$

Resolvemos con la fórmula general:

$$ k = \frac{-31 \pm \sqrt{31^2 - 4 \cdot 9 \cdot (-40)}}{2 \cdot 9} $$

$$ k = \frac{-31 \pm \sqrt{961 + 1440}}{18} = \frac{-31 \pm \sqrt{2401}}{18} = \frac{-31 \pm 49}{18} $$

De donde:

$$ k = \begin{cases} 1 \\[4pt] -\frac{40}{9} \end{cases} $$

Descartamos la solución negativa (por ser inadmisible en este contexto) y nos quedamos con $ a^2 = 1 $, de modo que:

$$ a = 1 $$

Sustituyendo en la primera ecuación:

$$ b^2 = 8 + a^2 = 9 \quad \Rightarrow \quad b = 3 $$

Con $ a = 1 $ y $ b = 3 $, la ecuación de la elipse es:

$$ \frac{x^2}{1} + \frac{y^2}{9} = 1 $$

$$ x^2 + \frac{y^2}{9} = 1 $$

Esta es la ecuación final de la elipse centrada en el origen que pasa por el punto dado y tiene como foco el punto especificado.

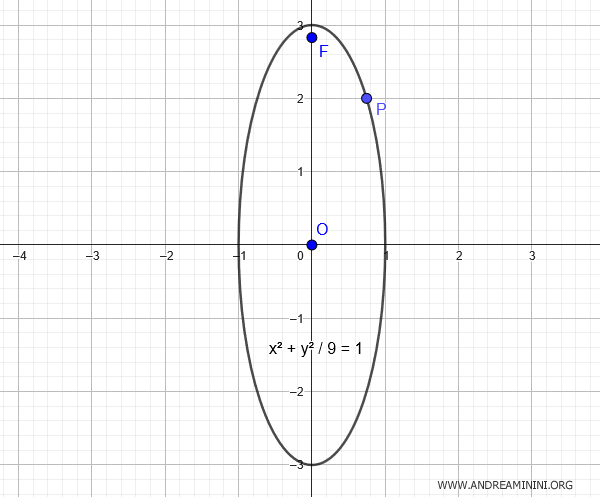
representación gráfica de la elipse

Así se determina paso a paso la ecuación de una elipse a partir de un punto y un foco conocidos.