Ecuación de una elipse no centrada en el origen de los ejes cartesianos
La ecuación de una elipse cuyo centro se encuentra en \( (x0, y0) \), es decir, fuera del origen del sistema de coordenadas cartesianas, se expresa mediante la forma canónica trasladada: $$ \frac{(x-x_0)^2}{a^2} + \frac{(y-y_0)^2}{b^2} = 1 $$.
También puede escribirse en la forma general:
$$ Ax^2 + By^2 + Cx + Dy + E = 0 $$
donde los coeficientes están relacionados con los parámetros de la elipse del siguiente modo:
$$ A = b^2 \qquad B = a^2 \qquad C = -2b^2x_0 \qquad D = -2a^2y_0 \qquad E = b^2x_0^2 + a^2y_0^2 - a^2b^2 $$
Las coordenadas del centro de la elipse quedan entonces dadas por:
$$ O \left( - \frac{C}{2A} ; - \frac{D}{2B} \right) $$
Por tanto, los ejes de simetría de la elipse son:
$$ x = - \frac{C}{2A} \qquad y = - \frac{D}{2B} $$
En definitiva, una elipse cuyo centro no está en el origen es simplemente una traslación de una elipse centrada en el origen.
Un ejemplo práctico
Consideremos una elipse con semiejes \(a = 3\) y \(b = 2\), y centro en el punto \((x_0, y_0) = (1, -2)\).
La ecuación en forma canónica trasladada, con \( x_0 = 1 \) y \( y_0 = -2 \), se escribe como:
$$ \frac{(x - x_0)^2}{a^2} + \frac{(y - y_0)^2}{b^2} = 1 $$
$$ \frac{(x - 1)^2}{3^2} + \frac{(y + 2)^2}{2^2} = 1 $$
$$ \frac{(x - 1)^2}{9} + \frac{(y + 2)^2}{4} = 1 $$
Veamos su representación gráfica:
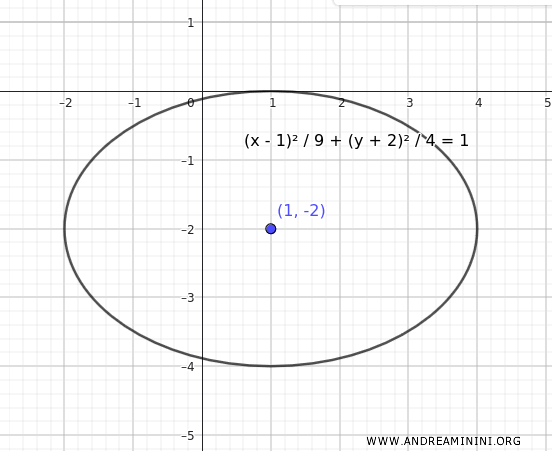
Observamos que se trata simplemente de una elipse centrada en el origen, desplazada hacia el punto \((1, -2)\).
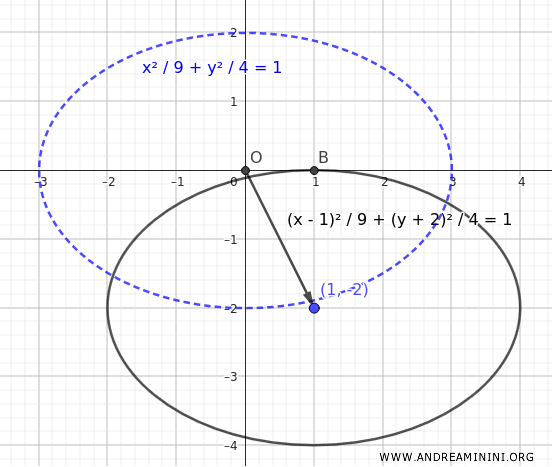
Pasemos ahora a obtener su forma general:
$$ Ax^2 + By^2 + Cx + Dy + E = 0 $$
Calculamos los coeficientes:
$$ A = b^2 = 2^2 = 4 $$
$$ B = a^2 = 3^2 = 9 $$
$$ C = -2b^2x_0 = -2 \cdot 4 \cdot 1 = -8 $$
$$ D = -2a^2y_0 = -2 \cdot 9 \cdot (-2) = 36 $$
$$ E = b^2x_0^2 + a^2y_0^2 - a^2b^2 = 4 \cdot 1^2 + 9 \cdot (-2)^2 - 9 \cdot 4 $$
$$ E = 4 + 36 - 36 = 4 $$
La ecuación general resultante es:
$$ 4x^2 + 9y^2 - 8x + 36y + 4 = 0 $$
La gráfica, evidentemente, no cambia:
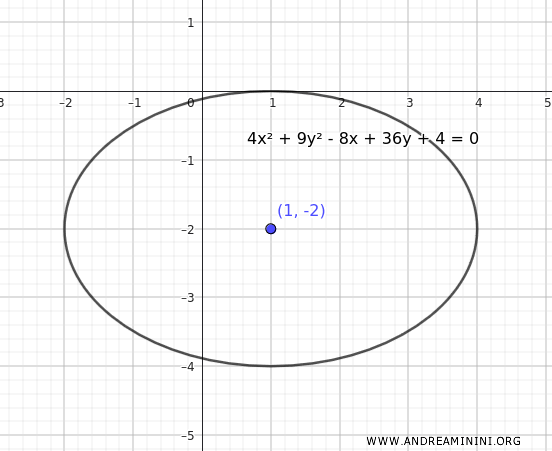
Verifiquemos ahora que el centro de la elipse es efectivamente \((1, -2)\), aplicando las fórmulas:
$$ h = -\frac{C}{2A} = -\frac{-8}{2 \cdot 4} = \frac{8}{8} = 1 $$
$$ k = -\frac{D}{2B} = -\frac{36}{2 \cdot 9} = -\frac{36}{18} = -2 $$
Confirmamos así que el centro es \((1, -2)\), como se esperaba.
En conclusión, tanto la forma canónica trasladada como la forma general describen la misma elipse con centro en \((1, -2)\) y semiejes \(a = 3\), \(b = 2\).
Demostración
Para demostrar la equivalencia entre la forma canónica y la forma general de una elipse no centrada en el origen, partimos de la ecuación estándar de una elipse con centro en el origen:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
Luego aplicamos una traslación, es decir, una transformación que conserva las distancias entre los puntos (una isometría):
$$ \begin{cases} x' = x + x_0 \\ y' = y + y_0 \end{cases} $$
Donde \(x'\) e \(y'\) son las nuevas coordenadas de cada punto, y \(x_0\), \(y_0\) representan los desplazamientos horizontal y vertical, respectivamente.
Despejamos las coordenadas originales:
$$ \begin{cases} x = x' - x_0 \\ y = y' - y_0 \end{cases} $$
Sustituimos en la ecuación original:
$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $$
$$ \frac{(x' - x_0)^2}{a^2} + \frac{(y' - y_0)^2}{b^2} = 1 $$
Desarrollamos los términos cuadráticos:
$$ \frac{x'^2 - 2x'x_0 + x_0^2}{a^2} + \frac{y'^2 - 2y'y_0 + y_0^2}{b^2} = 1 $$
Multiplicamos por el mínimo común denominador:
$$ \frac{b^2 (x'^2 - 2x'x_0 + x_0^2) + a^2 (y'^2 - 2y'y_0 + y_0^2)}{a^2b^2} = 1 $$
Multiplicamos ambos lados por \(a^2b^2\):
$$ b^2 (x'^2 - 2x'x_0 + x_0^2) + a^2 (y'^2 - 2y'y_0 + y_0^2) = a^2b^2 $$
Llevamos todos los términos al primer miembro:
$$ b^2 (x'^2 - 2x'x_0 + x_0^2) + a^2 (y'^2 - 2y'y_0 + y_0^2) - a^2b^2 = 0 $$
Desarrollamos los productos:
$$ x'^2b^2 - 2x'x_0b^2 + x_0^2b^2 + y'^2a^2 - 2y'y_0a^2 + y_0^2a^2 - a^2b^2 = 0 $$
Reordenamos los términos:
$$ x'^2 \cdot b^2 + y'^2 \cdot a^2 + x' \cdot (-2x_0b^2) + y' \cdot (-2y_0a^2) + x_0^2b^2 + y_0^2a^2 - a^2b^2 = 0 $$
Reconocemos los coeficientes:
$$ A = b^2,\quad B = a^2,\quad C = -2b^2x_0,\quad D = -2a^2y_0,\quad E = b^2x_0^2 + a^2y_0^2 - a^2b^2 $$
Entonces:
$$ Ax'^2 + By'^2 + Cx' + Dy' + E = 0 $$
Hemos obtenido así la forma general de la ecuación de una elipse centrada en \((x_0, y_0)\).
Y así continúa el razonamiento.