Esferas de Dandelin
Las esferas de Dandelin son esferas inscritas dentro de un cono circular recto de doble hoja, cada una de ellas tangente en un punto \( F \) a un plano secante \( p \).
El plano \( p \) no pasa por el vértice \( V \) del cono.
Según el ángulo de semiapertura del cono \( \alpha \) y el ángulo de inclinación del plano \( \beta \), se pueden presentar tres situaciones:
- Si \( \alpha > \beta \), se inscriben dos esferas de Dandelin, una en cada hoja del cono, y ambas son tangentes al plano en los puntos \( F_1 \) y \( F_2 \).
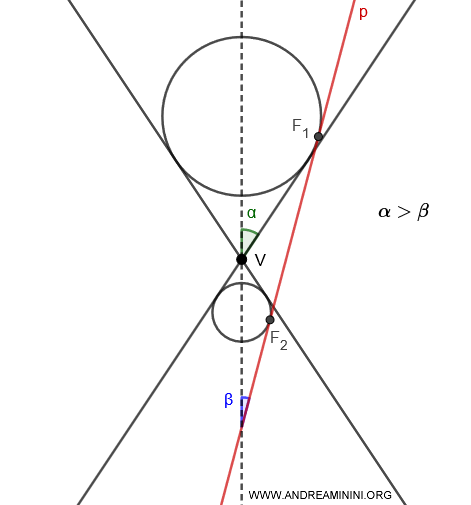
- Si \( \alpha = \beta \), hay una única esfera de Dandelin inscrita en la hoja del cono que es cortada por el plano \( p \).
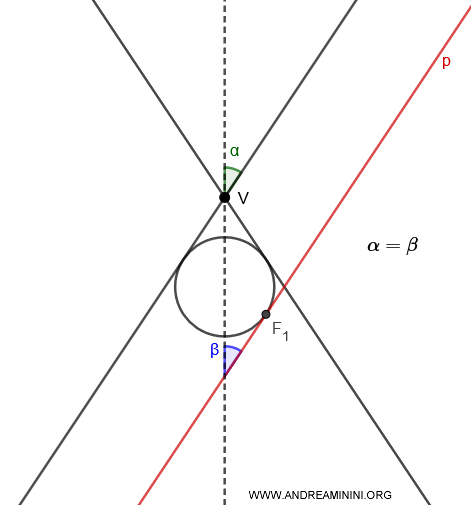
- Si \( \alpha < \beta \), se inscriben dos esferas de Dandelin dentro de la misma hoja del cono intersectada por el plano \( p \), siendo tangentes al plano en los puntos \( F_1 \) y \( F_2 \).
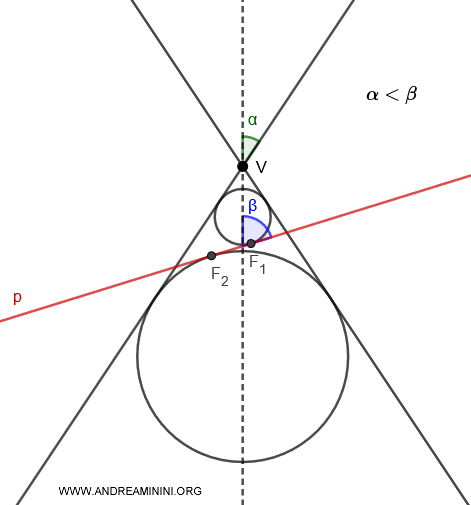
Esta vista lateral esquemática del cono y del plano se utiliza para ilustrar mejor el concepto.
En realidad, las esferas de Dandelin son tangentes a todas las generatrices del cono, y los puntos de tangencia describen un círculo contenido en un plano perpendicular al eje del cono.
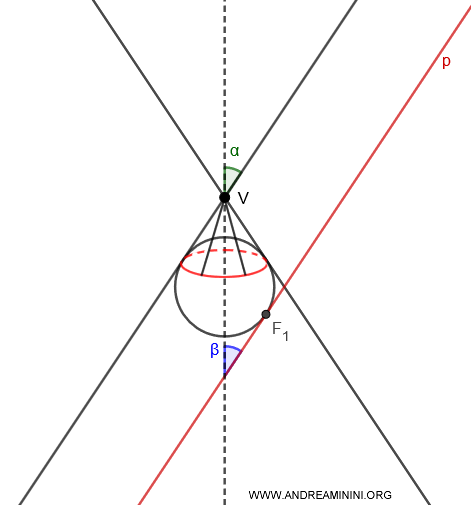
Nota: Los círculos se sitúan en planos perpendiculares (90°) al eje de simetría. No se encuentran sobre el eje que atraviesa el cono, el cual está inclinado con un ángulo \( \beta \).
Cuando dos esferas de Dandelin son tangentes a las generatrices de un mismo cono, la distancia entre los puntos de tangencia \( P_1 \) y \( P_2 \) permanece constante a lo largo de cada generatriz.
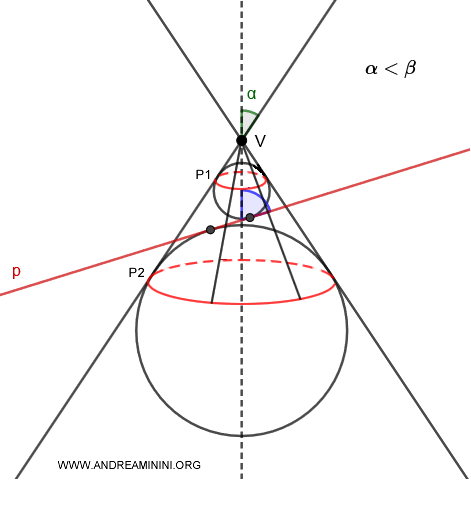
Las esferas de Dandelin, introducidas por el matemático Germinal Pierre Dandelin en 1822, constituyen una herramienta geométrica que permite demostrar ciertas propiedades fundamentales de las secciones cónicas (elipse, parábola e hipérbola).
Las secciones cónicas (elipse, parábola e hipérbola) son las curvas que se generan al cortar un cono con un plano.
- Elipse: cuando el plano corta una sola hoja del cono, se forman dos esferas tangentes al plano en puntos distintos. Estos puntos son los focos de la elipse.
- Parábola: si el plano es paralelo a una generatriz del cono, se inscribe una sola esfera que es tangente al plano en un único punto, el cual es el foco de la parábola.
- Hipérbola: cuando el plano intersecta ambas hojas del cono, se inscriben dos esferas que son tangentes al plano en dos puntos distintos, que corresponden a los focos de la hipérbola.
Así, las esferas de Dandelin ofrecen un enfoque geométrico para justificar propiedades clave de las cónicas, que habitualmente se abordan mediante métodos algebraicos.
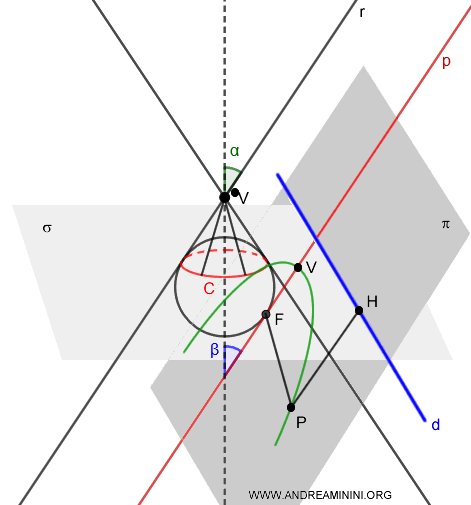
La excentricidad de una sección cónica depende del semiángulo \( \alpha \) del cono y del ángulo \( \beta \) que forma el plano secante con respecto al eje del cono.
$$ e = \frac{ \overline{PF} }{ \overline{PH} } = \frac{\cos \alpha }{ \cos \beta} $$
En esta expresión, \( \overline{PF} \) es la distancia desde un punto \( P \) sobre la cónica al foco \( F \), y \( \overline{PH} \) es la distancia desde el mismo punto \( P \) a la directriz \( d \).
La directriz \( d \) se obtiene como la intersección entre el plano \( \pi \) y el plano \( \sigma \), que es perpendicular al eje de simetría del cono.
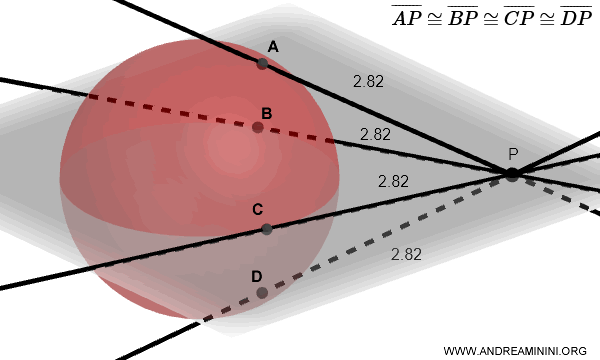
Nota: Un teorema muy útil en las demostraciones relacionadas con las esferas de Dandelin establece que todos los segmentos tangentes trazados desde un punto exterior \( P \) a una esfera son congruentes, es decir: \( \overline{AP} \cong \overline{BP} \cong \overline{CP} \cong \overline{DP} \)
Teorema de Dandelin para la Elipse
Cuando un plano corta una sola hoja de un cono y dos esferas inscritas son tangentes al plano en puntos distintos \( F_1 \) y \( F_2 \), estos puntos coinciden con los focos de la elipse formada. Los vértices de la elipse se encuentran en los puntos A y B.
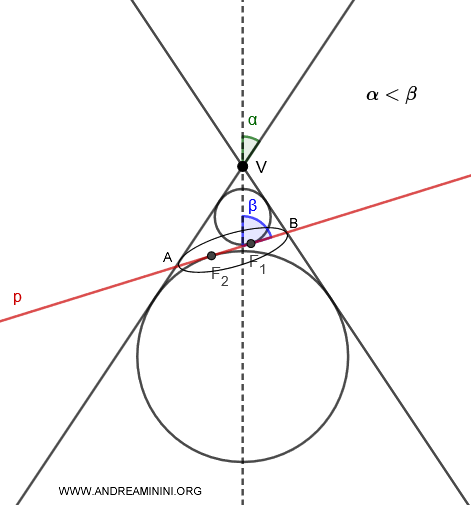
Para cualquier punto \( P \) sobre la elipse, la suma de las distancias a los focos \( \overline{PF_1} \) y \( \overline{PF_2} \) es constante e igual a la longitud del segmento AB:
$$ \overline{PF_1} + \overline{PF_2} = \overline{AB} $$
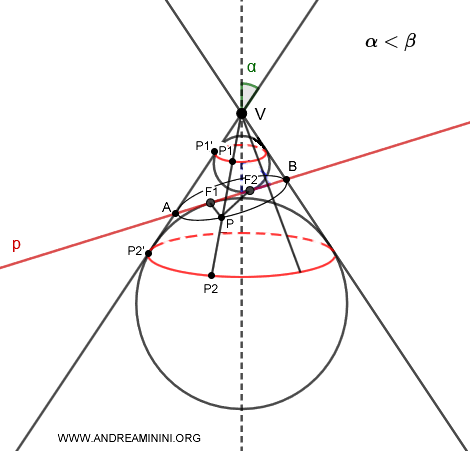
Demostración
Los segmentos que conectan los puntos donde las generatrices del cono cortan los dos círculos (perpendiculares al eje de simetría) son congruentes, ya que se trazan desde un mismo punto exterior \( V \), situado fuera de las esferas.
$$ \overline{P_1P_2} \cong \overline{P_1'P_2'} $$
Cada uno de estos segmentos, que une los dos círculos, corta la elipse y se compone de la suma de dos partes:
$$ \overline{P_1P_2} = \overline{P_1P} + \overline{PP_2} $$
En cualquier punto \( P \) de la elipse, se cumple que:
$$ \overline{PF_1} + \overline{PF_2} = k $$
Consideremos ahora el caso en que \( P \) coincide con uno de los vértices A o B:
$$ \overline{AF_1} + \overline{AF_2} = \overline{BF_1} + \overline{BF_2} = k $$
Queremos hallar el valor de la constante \( k \).
Dado que \( \overline{AB} = \overline{AF_2} + \overline{BF_2} \), se deduce que \( \overline{AF_2} = \overline{AB} - \overline{BF_2} \).
$$ \overline{AF_1} + \overline{AF_2} = \overline{BF_1} + \overline{BF_2} $$
$$ \overline{AF_1} + (\overline{AB} - \overline{BF_2}) = \overline{BF_1} + \overline{BF_2} $$
$$ \overline{AF_1} + \overline{AB} - \overline{BF_2} = \overline{BF_1} + \overline{BF_2} $$
$$ \overline{AF_1} + \overline{AB} - \overline{BF_1} = 2\overline{BF_2} $$
Como \( \overline{AB} - \overline{BF_1} = \overline{AF_1} \), se sigue que:
$$ \overline{AF_1} + \overline{AF_1} = 2\overline{BF_2} $$
$$ 2 \overline{AF_1} = 2\overline{BF_2} $$
Dividiendo ambos términos por dos:
$$ \overline{AF_1} = \overline{BF_2} $$
Con lo cual queda demostrado que \( \overline{AF_1} \) y \( \overline{BF_2} \) son segmentos congruentes.
Retomando la ecuación anterior, donde \( k \) todavía no se conoce:
$$ \overline{AF_1} + \overline{AF_2} = \overline{BF_1} + \overline{BF_2} = k $$
Sabemos que \( \overline{AF_2} = \overline{AF_1} + \overline{F_1F_2} \):
$$ \overline{AF_1} + (\overline{AF_1} + \overline{F_1F_2}) = \overline{BF_1} + \overline{BF_2} = k $$
Como también \( \overline{AF_1} = \overline{BF_2} \), resulta que:
$$ \overline{AF_1} + \overline{BF_2} + \overline{F_1F_2} = \overline{BF_1} + \overline{BF_2} = k $$
Pero la suma \( \overline{AF_1} + \overline{F_1F_2} + \overline{BF_2} \) es exactamente \( \overline{AB} \)
$$ \overline{AB} = \overline{BF_1} + \overline{BF_2} = k $$
Por lo tanto, la constante \( k \) es igual a la longitud del segmento AB.
$$ k = \overline{AB} $$
Y dado que la constante \( k \) se mantiene invariante para cualquier punto \( P \) sobre la elipse, se concluye que:
$$ \overline{PF_1} + \overline{PF_2} = \overline{AB} $$
Tal como ocurre en toda elipse.
Teorema de Dandelin para la Parábola
Cuando un plano secante \( \pi \) es paralelo a una generatriz \( r \) de un cono, existe una única esfera inscrita en su interior que es tangente al plano en un solo punto \( F \). Este punto \( F \) corresponde al foco de la parábola trazada sobre el plano \( \pi \).
La directriz \( d \) de la parábola se obtiene como intersección entre el plano secante \( \pi \) y otro plano \( \sigma \), perpendicular al eje del cono, que contiene el círculo \( C \) formado por los puntos de tangencia entre la esfera y el cono.

Para cualquier punto \( P \) perteneciente a la parábola se cumple la igualdad:
$$ \overline{PH} = \overline{PF} $$
Aquí, \( \overline{PH} \) representa la distancia entre el punto \( P \) y su proyección ortogonal \( H \) sobre la directriz, mientras que \( \overline{PF} \) es la distancia desde \( P \) al foco \( F \).
Este teorema constituye una demostración geométrica del hecho de que una parábola puede definirse como el conjunto de los puntos equidistantes de un punto fijo (el foco) y una recta (la directriz), partiendo directamente de su construcción como sección cónica.
Demostración
Tomemos un punto arbitrario \( P \) sobre la parábola.
Una generatriz \( g \) del cono pasa por \( P \) y corta el círculo \( C \) en el punto \( T \).
Consideremos ahora otro círculo \( C_2 \), situado en un plano perpendicular al eje de simetría del cono y que también contiene el punto \( P \).
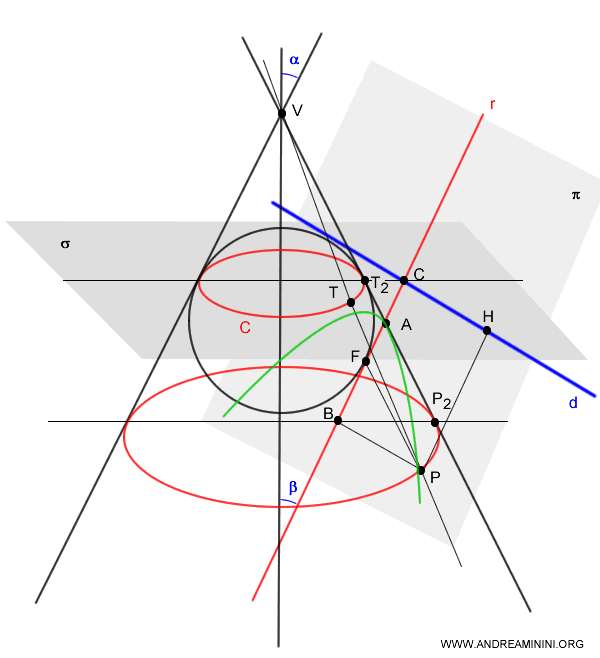
Los segmentos \( \overline{PT} \) y \( \overline{P_2T_2} \) son congruentes, ya que ambos círculos \( C \) y \( C_2 \) se encuentran en planos perpendiculares al eje del cono y las generatrices se originan en el mismo vértice \( V \).
$$ \overline{PT} \cong \overline{P_2T_2} $$
Sea \( B \) la proyección ortogonal de \( P \) sobre el eje de simetría \( p \), y \( H \) su proyección sobre la directriz \( d \).
El cuadrilátero \( CBPH \) que se forma es un rectángulo.
En todo rectángulo, los lados opuestos son iguales:
$$ \overline{BC} \cong \overline{PH} $$
$$ \overline{BP} \cong \overline{CH} $$
Por hipótesis, el ángulo semivertical \( \alpha \) del cono coincide con el ángulo de inclinación \( \beta \) del plano \( \pi \):
$$ \alpha \cong \beta $$
Esto implica que los triángulos \( ACT_2 \) y \( ABP_2 \) son semejantes y ambos isósceles.
Como consecuencia, los segmentos \( \overline{P_1T_1} \) y \( \overline{BC} \) resultan congruentes:
$$ \overline{P_1T_1} \cong \overline{BC} $$
Como \( \overline{PF} \) y \( \overline{PT} \) son segmentos tangentes desde un mismo punto \( P \) a la esfera, deben ser iguales:
$$ \overline{PF} \cong \overline{PT} $$
Dado que \( \overline{PT} \cong \overline{P_1T_1} \) y \( \overline{P_1T_1} \cong \overline{BC} \), entonces:
$$ \overline{PF} \cong \overline{BC} $$
Y como \( \overline{BC} \cong \overline{PH} \), se concluye que:
$$ \overline{PF} \cong \overline{PH} $$
Esto demuestra que, para todo punto \( P \) sobre la parábola, la distancia al foco es igual a su distancia a la directriz.
Nota: Incluso cuando \( P \) coincide con el vértice \( A \) de la parábola, la relación \( PF \cong PH \) sigue siendo válida. Como el triángulo \( ACT_2 \) es isósceles, sus lados oblicuos son congruentes \( \overline{AC} \cong \overline{AT_2} \). Además, \( \overline{AT_2} \cong \overline{AF} \), ya que ambos parten de \( A \) y son tangentes a la esfera. Por lo tanto, cuando \( P = A \) y su proyección es \( H = C \), se cumple \( AF \cong AC \), es decir, \( PF \cong PH \).
Teorema de Dandelin para la Hipérbola
Cuando un plano intersecta ambas hojas de un cono, se pueden inscribir dos esferas que resultan tangentes al plano. Los puntos de tangencia son los focos de la hipérbola generada.
Para cualquier punto \( P \) de la hipérbola se cumple la siguiente relación:
$$ | \overline{PF_1} - \overline{PF_2} | = \overline{AB} $$
donde \( A \) y \( B \) son los vértices de la hipérbola.
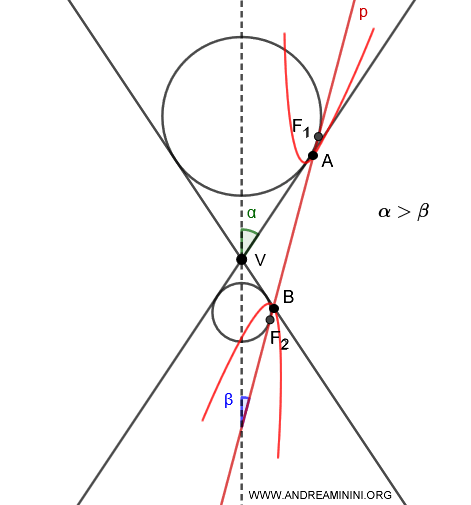
Demostración
Consideremos un punto \( P \) sobre la hipérbola, que se encuentra sobre una generatriz \( g \) del cono.
Dicha generatriz corta los círculos \( C_1 \) y \( C_2 \), asociados a las esferas inscritas, en los puntos \( P_1 \) y \( P_2 \).
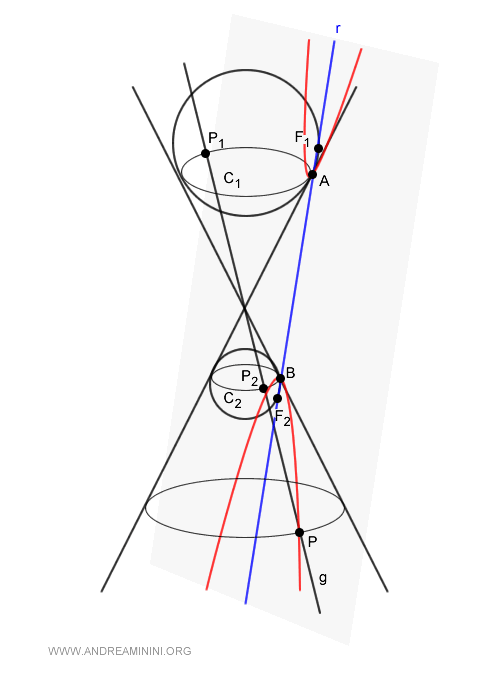
Los segmentos \( \overline{PF_1} \) y \( \overline{PP_1} \) son congruentes porque son tangentes a la misma esfera y parten del mismo punto \( P \):
$$ \overline{PF_1} \cong \overline{PP_1} $$
De manera análoga:
$$ \overline{PF_2} \cong \overline{PP_2} $$
Por tanto, la diferencia entre ambas distancias equivale a:
$$ | \overline{PF_1} - \overline{PF_2} | = | \overline{PP_1} - \overline{PP_2} | $$
La cantidad \( | \overline{PP_1} - \overline{PP_2} | \) corresponde al segmento \( \overline{P_1P_2} \), que permanece constante para todos los puntos situados sobre los círculos \( C_1 \) y \( C_2 \):
$$ | \overline{PF_1} - \overline{PF_2} | = \overline{P_1P_2} $$
Si ahora tomamos \( P = A \), vértice de la hipérbola:
$$ | \overline{AF_1} - \overline{AF_2} | = \overline{P_1P_2} $$
Y también en \( P = B \):
$$ | \overline{BF_2} - \overline{BF_1} | = \overline{P_1P_2} $$
De aquí se deduce:
$$ | \overline{AF_1} - \overline{AF_2} | = | \overline{BF_2} - \overline{BF_1} | $$
Sabemos que \( \overline{AF_2} = \overline{F_1F_2} - \overline{AF_1} \), y que \( \overline{BF_1} = \overline{F_1F_2} - \overline{BF_2} \). Por lo tanto:
$$ | \overline{AF_1} - (\overline{F_1F_2} - \overline{AF_1}) | = | \overline{BF_2} - (\overline{F_1F_2} - \overline{BF_2}) | $$
$$ | 2 \overline{AF_1} - \overline{F_1F_2} | = | 2 \overline{BF_2} - \overline{F_1F_2} | $$
Al eliminar \( \overline{F_1F_2} \) de ambos lados, se obtiene:
$$ 2 \overline{AF_1} = 2 \overline{BF_2} $$
Y dividiendo entre dos:
$$ \overline{AF_1} = \overline{BF_2} $$
Volviendo a la diferencia original:
$$ | \overline{AF_1} - \overline{AF_2} | = | \overline{BF_2} - \overline{AF_2} | $$
Y como \( \overline{AF_2} - \overline{BF_2} = \overline{AB} \), tenemos:
$$ | \overline{AF_1} - \overline{AF_2} | = \overline{AB} $$
Queda demostrado, por tanto, que para cualquier punto \( P \) sobre la hipérbola, la diferencia absoluta entre sus distancias a los focos es igual a la distancia entre los vértices:
$$ | \overline{PF_1} - \overline{PF_2} | = \overline{AB} $$
Lo cual completa la demostración.