Las circunferencias tangentes
Se denomina circunferencias tangentes a aquellas que se intersectan en un único punto.
Ese punto común recibe el nombre de punto de tangencia o punto de contacto.
Las circunferencias pueden ser tangentes de dos formas:
- Circunferencias tangentes interiormente
Dos circunferencias son tangentes interiormente cuando una se encuentra completamente dentro de la otra y se tocan en un único punto. Esto ocurre cuando el centro de una de ellas está ubicado en el interior de la otra.
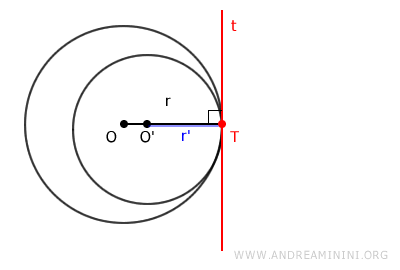
Si los radios de las dos circunferencias son \( r_1 \) y \( r_2 \), y la distancia entre sus centros es \( d \), la condición para que sean tangentes interiormente es: \[ d = |r_1 - r_2| \]Cálculo de la distancia entre los centros. Para determinar la distancia entre los centros se utiliza la fórmula de la distancia euclídea entre dos puntos en el plano: \[ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \] donde \( (x_1, y_1) \) y \( (x_2, y_2) \) son las coordenadas de los centros \( C_1 \) y \( C_2 \) en el plano cartesiano.
- Circunferencias tangentes exteriormente
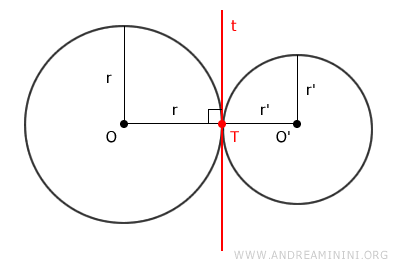
Este caso se da cuando el centro de cada circunferencia está situado fuera de la otra. En otras palabras, el punto de tangencia se ubica entre ambas circunferencias, sobre la recta que une sus centros.
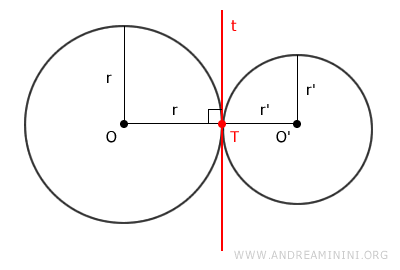
Para que dos circunferencias sean tangentes exteriormente, la suma de sus radios \( r_1 + r_2 \) debe ser igual a la distancia \( d \) que separa sus centros: \[ d = r_1 + r_2 \]
En ambos casos, las circunferencias tangentes comparten un punto común \( T \) y la misma recta tangente \( t \).
Cómo hallar el punto de tangencia
El punto de tangencia \( T \) se localiza sobre la recta que une los dos centros.
Si las circunferencias son tangentes exteriormente, las coordenadas de \( T \) se calculan empleando la proporción entre los radios y la distancia \( d \):
$$ T = \left( x_1 + \frac{r_1}{r_1 + r_2}(x_2 - x_1), y_1 + \frac{r_1}{r_1 + r_2}(y_2 - y_1) \right) $$
Si las circunferencias son tangentes interiormente, las coordenadas de \( T \) se obtienen utilizando la proporción inversa entre los radios y la distancia \( d \):
$$ T = \left( x_1 + \frac{r_1}{r_1 - r_2}(x_2 - x_1), y_1 + \frac{r_1}{r_1 - r_2}(y_2 - y_1) \right) $$
Otra forma de determinar el punto de tangencia es plantear un sistema de ecuaciones a partir de las ecuaciones de ambas circunferencias: $$ \begin{cases} (x - x_1)^2 + (y - y_1)^2 = r_1^2 \\ \\ (x - x_2)^2 + (y - y_2)^2 = r_2^2 \end{cases} $$ o bien $$ \begin{cases} x^2 + y^2 + ax + by + c = 0 \\ \\ x^2 + y^2 + a'x + b'y + c' = 0 \end{cases} $$ Posteriormente, se resuelve el sistema mediante el método de reducción, restando la primera ecuación a la segunda. $$ \begin{cases} x^2 + y^2 + ax + by + c = 0 \\ \\ (a' - a)x + (b' - b)y + (c' - c) = 0 \end{cases} $$ La segunda ecuación corresponde al eje radical de las dos circunferencias, que, en el caso de circunferencias tangentes, coincide con la recta tangente que las une. Una vez obtenido esto, basta resolver el sistema para encontrar las coordenadas \( x \) e \( y \) del punto de tangencia.
Conocido el punto de tangencia \( T \), también es posible hallar la ecuación de la recta tangente utilizando la fórmula de la tangente a una circunferencia.
La ecuación de la recta tangente a la circunferencia \( (x - x_0)^2 + (y - y_0)^2 = r^2 \), cuyo centro es \( C(x_0, y_0) \) y radio \( r \), en el punto \( T = (x_T, y_T) \), es:
$$ (x_T - x_0)(x - x_0) + (y_T - y_0)(y - y_0) = r^2 $$
Un ejemplo práctico
Veamos un ejemplo concreto con dos circunferencias:
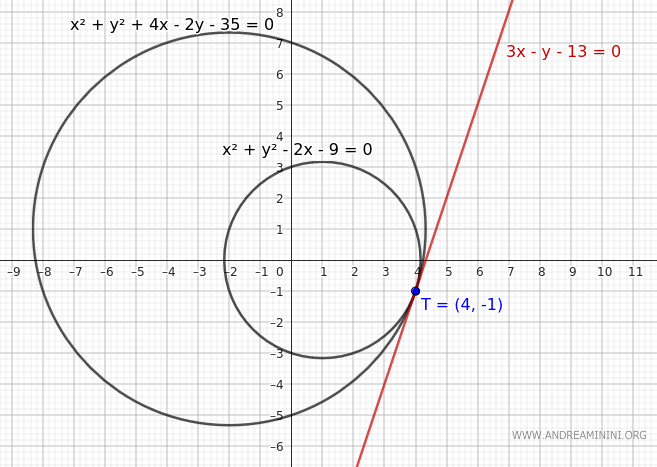
$$ x^2 + y^2 - 2x - 9 = 0 $$
$$ C_2: x^2 + y^2 + 4x - 2y - 35 = 0 $$
El centro y el radio de la primera circunferencia se obtienen a partir de los coeficientes a = -2, b = 0 y c = -9:
$$ C_1 \left( -\frac{a}{2}, -\frac{b}{2} \right) = \left( -\frac{-2}{2}, -\frac{0}{2} \right) = (1, 0) $$
$$ r_1 = \sqrt{ \left( -\frac{a}{2} \right)^2 + \left( -\frac{b}{2} \right)^2 - c } = \sqrt{1 - 0 - (-9)} = \sqrt{10} $$
Aplicando el mismo procedimiento, hallamos el centro y el radio de la segunda circunferencia. En este caso, los coeficientes son a = 4, b = -2 y c = -35:
$$ C_2 \left( -\frac{a}{2}, -\frac{b}{2} \right) = \left( -\frac{4}{2}, -\frac{-2}{2} \right) = (-2, 1) $$
$$ r_2 = \sqrt{ \left( -\frac{a}{2} \right)^2 + \left( -\frac{b}{2} \right)^2 - c } = \sqrt{(-2)^2 + (1)^2 - (-35)} = \sqrt{4 + 1 + 35} = \sqrt{40} $$
Con las coordenadas de los centros \( C_1 (1, 0) \) y \( C_2 (-2, 1) \) conocidas, calculamos la distancia euclídea que los separa:
$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} $$
$$ d = \sqrt{(-2 - 1)^2 + (1 - 0)^2} $$
$$ d = \sqrt{(-3)^2 + (1)^2} $$
$$ d = \sqrt{9 + 1} $$
$$ d = \sqrt{10} $$
A continuación, calculamos la suma y la diferencia absoluta de los radios:
$$ r_1 + r_2 = \sqrt{10} + \sqrt{40} = \sqrt{10} + \sqrt{4 \cdot 10} = \sqrt{10} + 2 \sqrt{10} = 3 \sqrt{10} $$
$$ | r_1 - r_2 | = | \sqrt{10} - \sqrt{40} | = | \sqrt{10} - 2 \sqrt{10} | = | -\sqrt{10} | = \sqrt{10} $$
Observamos que, en este caso, la distancia entre los centros \( d = \sqrt{10} \) coincide con el valor absoluto de la diferencia entre los radios:
$$ d = | r_1 - r_2 | = \sqrt{10} $$
Por tanto, las dos circunferencias son tangentes interiormente.
Las coordenadas del punto de tangencia se calculan mediante la siguiente expresión:
$$ T = \left( x_1 + \frac{r_1}{r_1 - r_2}(x_2 - x_1),\; y_1 + \frac{r_1}{r_1 - r_2}(y_2 - y_1) \right) $$
Con \( r_1 = \sqrt{10} \) y \( r_2 = \sqrt{40} \), tenemos:
$$ T = \left( x_1 + \frac{\sqrt{10}}{\sqrt{10} - \sqrt{40}}(x_2 - x_1),\; y_1 + \frac{\sqrt{10}}{\sqrt{10} - \sqrt{40}}(y_2 - y_1) \right) $$
Usando los centros \( C_1(x_1, y_1) = (1, 0) \) y \( C_2(x_2, y_2) = (-2, 1) \):
$$ T = \left( 1 + \frac{\sqrt{10}}{\sqrt{10} - \sqrt{40}}(-2 - 1),\; 0 + \frac{\sqrt{10}}{\sqrt{10} - \sqrt{40}}(1 - 0) \right) $$
$$ T = \left( 1 + \frac{\sqrt{10}}{\sqrt{10} - 2\sqrt{10}}(-3),\; 0 + \frac{\sqrt{10}}{\sqrt{10} - 2\sqrt{10}}(1) \right) $$
$$ T = \left( 1 + \frac{\sqrt{10}}{-\sqrt{10}}(-3),\; 0 + \frac{\sqrt{10}}{\sqrt{10} - 2\sqrt{10}}(1) \right) $$
$$ T = \left( 1 + \frac{\sqrt{10}}{-\sqrt{10}}(-3),\; 0 + \frac{1}{1 - 2} \right) $$
$$ T = \left( 1 + 3,\; 0 - 1 \right) $$
$$ T = \left( 4,\; -1 \right) $$
Conocido el punto de tangencia \( T = (4, -1) \), podemos hallar también la ecuación de la recta tangente.
$$ (x_T - x_0)(x - x_0) + (y_T - y_0)(y - y_0) = r^2 $$
$$ (4 - x_0)(x - x_0) + (-1 - y_0)(y - y_0) = r^2 $$
Escogemos el centro y radio de una de las dos circunferencias, normalmente la más sencilla. Por ejemplo, \( C_1(1, 0) \) y \( r_1 = \sqrt{10} \):
$$ (4 - 1)(x - 1) + (-1 - 0)(y - 0) = (\sqrt{10})^2 $$
$$ 3(x - 1) - y = 10 $$
$$ 3x - 3 - y - 10 = 0 $$
$$ 3x - y - 13 = 0 $$
Esta es la ecuación de la recta tangente que pasa por el punto \( T(4, -1) \).
Solución alternativa
Consideremos de nuevo las dos circunferencias del ejemplo:
$$ x^2 + y^2 - 2x - 9 = 0 $$
$$ x^2 + y^2 + 4x - 2y - 35 = 0 $$
Planteamos un sistema de ecuaciones a partir de las ecuaciones de ambas circunferencias:
$$ \begin{cases} x^2 + y^2 - 2x - 9 = 0 \\ \\ x^2 + y^2 + 4x - 2y - 35 = 0 \end{cases} $$
Aplicamos el método de reducción, restando la primera ecuación de la segunda:
$$ \begin{cases} x^2 + y^2 - 2x - 9 = 0 \\ \\ x^2 + y^2 + 4x - 2y - 35 - (x^2 + y^2 - 2x - 9) = 0 \end{cases} $$
$$ \begin{cases} x^2 + y^2 - 2x - 9 = 0 \\ \\ 6x - 2y - 26 = 0 \end{cases} $$
$$ \begin{cases} x^2 + y^2 - 2x - 9 = 0 \\ \\ 3x - y - 13 = 0 \end{cases} $$
La ecuación \( 3x - y - 13 = 0 \) representa el eje radical, que coincide con la recta tangente en el caso de circunferencias tangentes.
Así, el sistema inicial equivale al formado por la ecuación de una circunferencia y la del eje radical:
$$ \begin{cases} x^2 + y^2 - 2x - 9 = 0 \\ \\ y = 3x - 13 \end{cases} $$
Sustituimos \( y \) en la ecuación de la circunferencia:
$$ \begin{cases} x^2 + (3x - 13)^2 - 2x - 9 = 0 \\ \\ y = 3x - 13 \end{cases} $$
$$ \begin{cases} x^2 + \big(9x^2 - 2 \cdot 3x \cdot 13 + 13^2\big) - 2x - 9 = 0 \\ \\ y = 3x - 13 \end{cases} $$
$$ \begin{cases} x^2 + (9x^2 - 78x + 169) - 2x - 9 = 0 \\ \\ y = 3x - 13 \end{cases} $$
$$ \begin{cases} 10x^2 - 80x + 160 = 0 \\ \\ y = 3x - 13 \end{cases} $$
$$ \begin{cases} x^2 - 8x + 16 = 0 \\ \\ y = 3x - 13 \end{cases} $$
Resolvemos ahora la ecuación cuadrática:
$$ \Delta = b^2 - 4ac = (-8)^2 - 4 \cdot 16 = 64 - 64 = 0 $$
La ecuación posee una única solución:
$$ x = \frac{-b \pm \sqrt{\Delta}}{2a} $$
$$ x = \frac{-(-8) \pm \sqrt{0}}{2 \cdot 1} $$
$$ x = \frac{8}{2} $$
$$ x = 4 $$
Una vez hallada la coordenada \( x \), sustituimos en la ecuación de la recta para obtener \( y \):
$$ y = 3x - 13 $$
$$ y = 3 \cdot 4 - 13 $$
$$ y = 12 - 13 $$
$$ y = -1 $$
Por tanto, el punto de tangencia entre ambas circunferencias es:
$$ T(4, -1) $$
A continuación, se muestra el gráfico de las circunferencias y la recta tangente.

Teorema de las circunferencias tangentes
La condición necesaria y suficiente para que dos circunferencias sean tangentes es la siguiente:
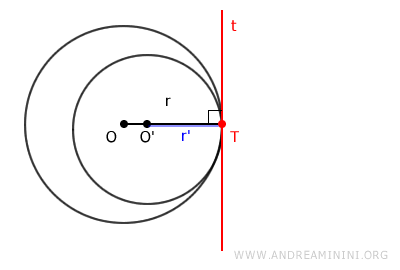
- La distancia entre los centros de las circunferencias es igual al valor absoluto de la diferencia de sus radios si son tangentes interiormente: $$ OO'=| r - r' | $$
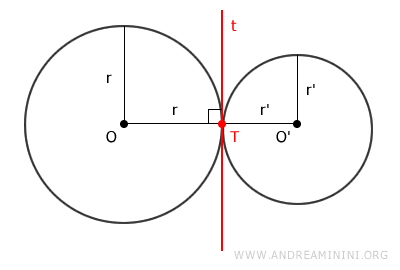
- La distancia entre los centros de las circunferencias es igual a la suma de sus radios si son tangentes exteriormente: $$ OO'=r + r' $$
Demostración
Consideremos dos circunferencias tangentes, la primera de radio \( r \) y la segunda de radio \( r' \), suponiendo que \( r \) es mayor que \( r' \).
Al ser tangentes, ambas circunferencias comparten un punto común T, que corresponde al punto de tangencia.
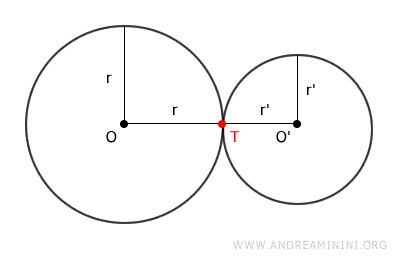
El punto \( T \) es el extremo del radio en ambas circunferencias:
$$ r = OT $$
$$ r' = O'T $$
En el punto de tangencia, pasa una recta \( t \) perpendicular al radio de la circunferencia.
Por lo tanto, en \( T \), la misma recta es perpendicular a ambos radios \( r \) y \( r' \).
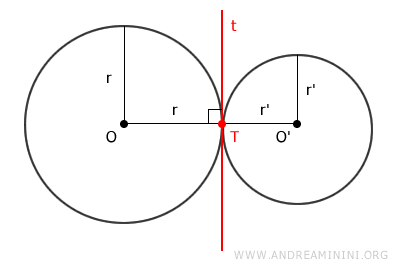
Como consecuencia, los puntos O, T y O' están alineados.
Dado que estos tres puntos están sobre la misma recta, se pueden presentar dos situaciones:
- Si la distancia entre los centros OO' = r + r' es igual a la suma de los radios, significa que el centro de cada circunferencia está fuera de la otra, por lo que son tangentes exteriormente.
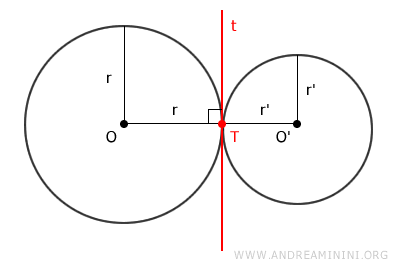
- Si la distancia entre los centros OO' = r - r' es igual a la diferencia de los radios, entonces el centro de una circunferencia está dentro de la otra, y son tangentes interiormente.
Notas
A continuación, algunas observaciones sobre las circunferencias tangentes:
- Cuando dos circunferencias son tangentes, el punto de tangencia \( T \) se encuentra sobre el segmento \( OO' \) que une los centros de ambas.
Demostración. Dos circunferencias tangentes tienen en común un único punto \( T \) (el punto de tangencia). Por \( T \) pasa una recta "t" perpendicular al radio. Dado que solo existe una recta perpendicular a un mismo segmento, se deduce que la recta tangente "t" es perpendicular a ambos radios \( OT \) y \( O'T \) de las dos circunferencias. En consecuencia, los centros de las circunferencias \( O \), \( O' \) y el punto de tangencia \( T \) están alineados, es decir, pertenecen al segmento \( OO' \) y, por tanto, a la misma recta.
Y así sucesivamente.