Teorema de la Distancia de una Recta al Centro de una Circunferencia
Una recta es secante, tangente o exterior a una circunferencia si su distancia al centro es menor, igual o mayor que el radio, respectivamente. Y viceversa.
Dicho de otro modo, pueden darse tres situaciones:
Si una recta está a una distancia del centro menor que el radio \( d < r \), se trata de una recta secante a la circunferencia.

Si una recta toca la circunferencia en un único punto, su distancia al centro es exactamente igual al radio \( d = r \), por lo que es una recta tangente.

Finalmente, si la recta se encuentra a una distancia del centro mayor que el radio \( d > r \), no corta la circunferencia en ningún punto, por lo que es una recta exterior.
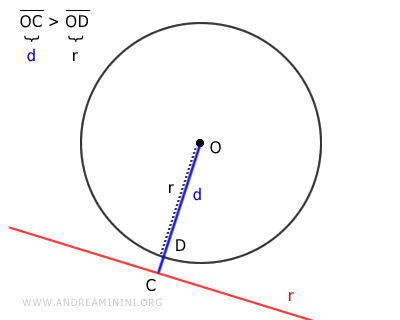
También se cumple el teorema recíproco: una recta secante, tangente o exterior mantiene, respectivamente, una distancia al centro menor, igual o mayor que el radio.
Cómo Determinar Algebraicamente los Puntos de Intersección
En geometría analítica, para averiguar si una recta es secante, tangente o exterior a una circunferencia, basta resolver el sistema formado por las ecuaciones de ambas.
$$ \begin{cases} x^2 + y^2 + ax + by + c = 0 \\ \\ a'x + b'y + c' = 0 \end{cases} $$
Las soluciones (x, y) de este sistema son las coordenadas de los puntos donde la recta intersecta la circunferencia.
En función del número de soluciones, pueden ocurrir tres casos:
- 0 soluciones: la recta es exterior a la circunferencia.
- 1 solución: la recta es tangente a la circunferencia.
- 2 soluciones: la recta es secante a la circunferencia.
Este procedimiento permite determinar algebraicamente el número de puntos de intersección, sin necesidad de representar gráficamente la circunferencia ni la recta.
Ejemplo Práctico
Consideremos una circunferencia y una recta. Queremos saber si la recta es secante, tangente o exterior a dicha circunferencia.
No disponemos del gráfico, sino únicamente de sus ecuaciones.
La ecuación de la circunferencia es:
$$ x^2 + y^2 - 6x - 4y + 4 = 0 $$
La ecuación de la recta es:
$$ x - y - 4 = 0 $$
Planteamos el sistema formado por ambas ecuaciones:
$$ \begin{cases} x^2 + y^2 - 6x - 4y + 4 = 0 \\ \\ x - y - 4 = 0 \end{cases} $$
Debemos comprobar si el sistema tiene soluciones y cuántas.
Usamos el método de sustitución: despejamos y en la segunda ecuación y lo sustituimos en la primera:
$$ \begin{cases} x^2 + (x - 4)^2 - 6x - 4(x - 4) + 4 = 0 \\ \\ y = x - 4 \end{cases} $$
$$ \begin{cases} x^2 + x^2 - 8x + 16 - 6x - 4x + 16 + 4 = 0 \\ \\ y = x - 4 \end{cases} $$
$$ \begin{cases} 2x^2 - 18x + 36 = 0 \\ \\ y = x - 4 \end{cases} $$
Podemos simplificar dividiendo la primera ecuación entre dos:
$$ \begin{cases} x^2 - 9x + 18 = 0 \\ \\ y = x - 4 \end{cases} $$
Estudiamos el discriminante Δ de la ecuación cuadrática:
$$ \Delta = b^2 - 4ac $$
$$ \Delta = (-9)^2 - 4 \cdot 1 \cdot 18 $$
$$ \Delta = 81 - 72 $$
$$ \Delta = 9 $$
Como el discriminante es positivo, el sistema tiene dos soluciones reales y distintas. Podemos concluir que la recta es secante a la circunferencia, pues la corta en dos puntos diferentes.
Nota: Analizando el discriminante, podemos determinar de inmediato el número de soluciones de la ecuación cuadrática en el sistema. Según el valor de Δ:
- Si Δ > 0, existen dos soluciones reales distintas, y la recta es secante a la circunferencia.
- Si Δ = 0, existe una única solución doble real, y la recta es tangente.
- Si Δ < 0, no hay soluciones reales, y la recta es exterior a la circunferencia.
¿Cuáles son las coordenadas de los puntos de intersección?
Dado que el discriminante es positivo (es decir, no estamos ante una recta exterior), podemos hallar las coordenadas (x, y) de los puntos de intersección.
Resolvemos la ecuación $ x^2 - 9x + 18 = 0 $:
$$ x = \frac{-b \pm \sqrt{\Delta}}{2a} $$
$$ x = \frac{-(-9) \pm \sqrt{9}}{2 \cdot 1} $$
$$ x = \frac{9 \pm 3}{2} = \begin{cases} x = \frac{9 - 3}{2} = 3 \\ \\ x = \frac{9 + 3}{2} = 6 \end{cases} $$
Por tanto, la primera ecuación del sistema tiene dos soluciones: x = 3 y x = 6.
$$ \begin{cases} 2x^2 - 18x + 36 = 0 \\ \\ y = x - 4 \end{cases} $$
Sustituimos los valores de x en la segunda ecuación para obtener los valores de y correspondientes:
$$ y = x - 4 = \begin{cases} y = 3 - 4 = -1 \\ \\ y = 6 - 4 = 2 \end{cases} $$
La primera solución del sistema es el par x = 3, y = -1.
La segunda solución es el par x = 6, y = 2.
Así, la recta corta a la circunferencia en los puntos (3, -1) y (6, 2).

En conclusión, este método nos permite determinar de manera algebraica la posición relativa de una recta respecto a una circunferencia, sin necesidad de realizar representaciones gráficas.
La Demostración
La demostración se desarrolla considerando tres casos distintos:
A] Distancia de la Recta Menor que el Radio
Consideremos una recta \( r \) y una circunferencia de centro \( O \) y radio \( OA \).
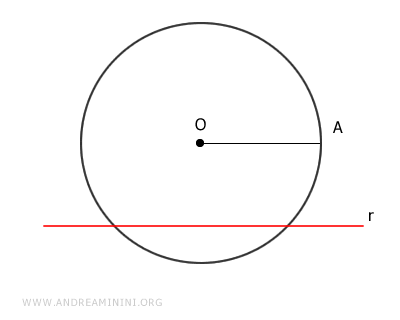
La distancia entre la recta y el centro \( O \) de la circunferencia está representada por el segmento \( OB \).
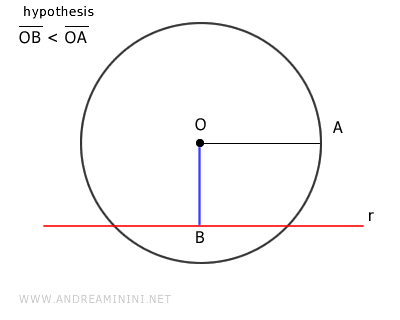
Por hipótesis inicial, la distancia de la recta al centro es menor que el radio.
$$ \overline{OB} < \overline{OA} $$
Sobre la recta \( r \), se construye un segmento \( BC \) cuya longitud es igual al radio \( OA \).
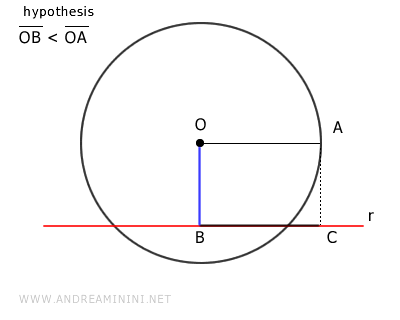
A continuación, se une el punto \( C \) con el centro \( O \) mediante el segmento \( OC \).
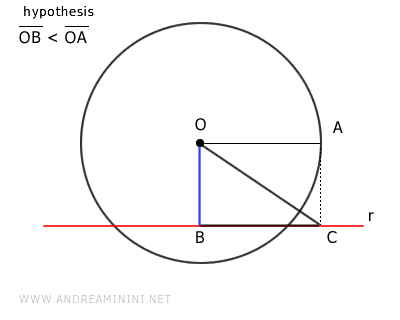
Se forma así el triángulo rectángulo \( OBC \).
En un triángulo rectángulo, la hipotenusa \( OC \) es siempre mayor que sus catetos \( OB \) y \( BC \). En particular, nos interesa que OC > BC:
$$ \overline{OC} > \overline{BC} $$
Dado que \( BC \cong OA \), se deduce que el segmento \( OC \) es mayor que el radio:
$$ \overline{OC} > \overline{OA} $$
Por lo tanto, el punto \( C \) se encuentra fuera de la circunferencia.
El segmento \( BC \) presenta un punto interior (B) y otro exterior (C) con respecto a la circunferencia.
En consecuencia, \( BC \) intersecta la circunferencia al menos en un punto \( D \).
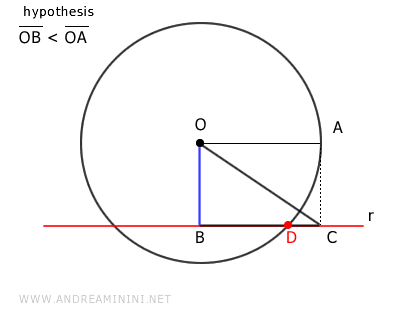
Se repite el mismo procedimiento en el lado opuesto de la recta.
Sobre la recta \( r \), se traza un segmento \( BE \) congruente con el radio \( OA \) de la circunferencia.
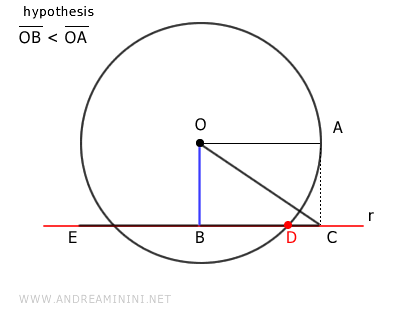
Después, se une el punto \( E \) con el centro \( O \) mediante el segmento \( OE \), formando así un triángulo rectángulo \( OBE \).
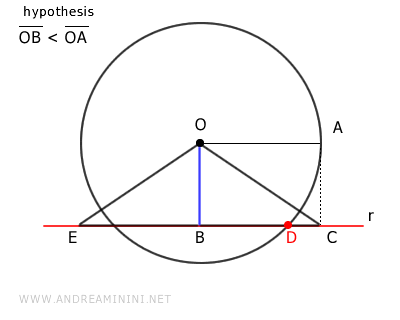
En este triángulo, la hipotenusa \( OE \) también es mayor que los catetos \( OB \) y \( EB \):
$$ \overline{OE} > \overline{EB} $$
El segmento \( EB \) posee un punto interior (B) y otro exterior (E) respecto a la circunferencia.
Por lo tanto, \( EB \) corta la circunferencia al menos en un punto \( F \).
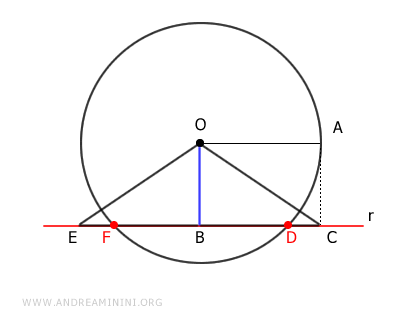
Con ello, se demuestra que la recta \( r \) corta a la circunferencia en dos puntos distintos \( D \) y \( F \).
Por lo tanto, la recta \( r \) es secante a la circunferencia.
B] Distancia de la Recta Igual al Radio
En este caso, por hipótesis inicial, la recta \( r \) se encuentra a una distancia del centro \( O \) exactamente igual al radio \( OA \).
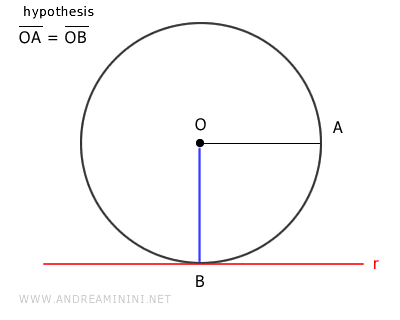
Es decir:
$$ \overline{OB} = \overline{OA} $$
Sobre la recta \( r \), se traza un segmento \( BC \) congruente con el radio \( OA \), es decir, BC \cong OA.
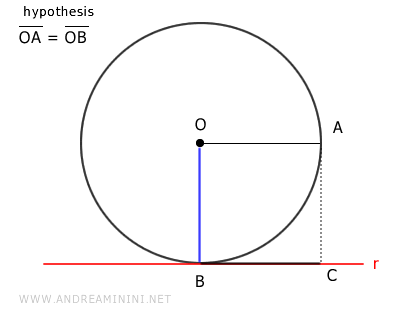
Se unen los puntos \( O \) y \( C \).
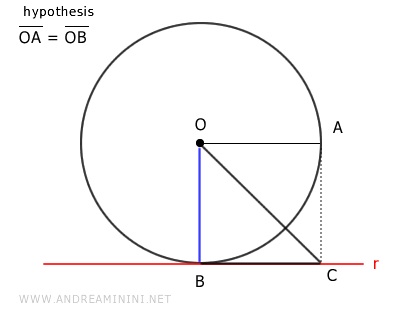
Así se obtiene el triángulo rectángulo \( OBC \).
En cualquier triángulo rectángulo, la hipotenusa es siempre mayor que cualquiera de los catetos. Por lo tanto, OC > BC:
$$ \overline{OC} > \overline{BC} $$
Dado que \( BC \cong OA \), se concluye que \( OC \) es mayor que el radio \( OA \):
$$ \overline{OC} > \overline{OA} $$
Por tanto, el punto \( C \) se encuentra fuera de la circunferencia.
Esto implica que el segmento \( BC \) tiene un punto interior (B) y uno exterior (C) con respecto a la circunferencia.
Por ello, intersecta la circunferencia al menos en el punto \( B \).
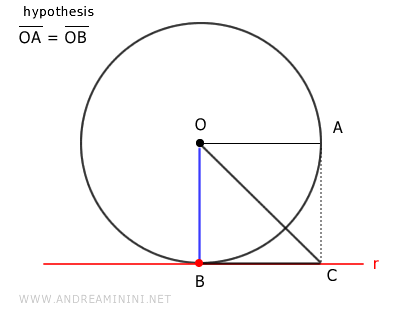
Se repite el mismo razonamiento en el otro lado.
Se construye un segmento \( BD \) sobre la recta \( r \) tal que \( BD \cong OA \), es decir, congruente con el radio de la circunferencia.
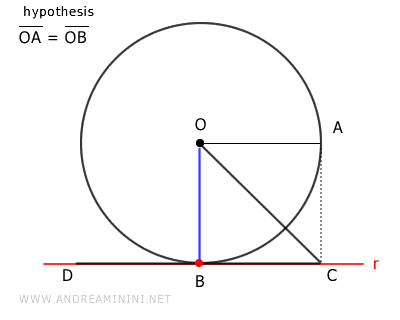
Se unen los puntos \( O \) y \( D \).
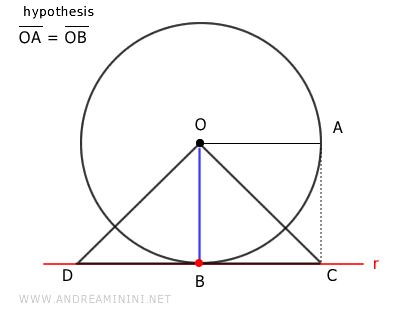
El triángulo \( OBD \) también es rectángulo.
Por lo tanto, la hipotenusa \( OD \) es mayor que el cateto \( BD \):
$$ \overline{OD} > \overline{BD} $$
Así, el segmento \( OD \) resulta mayor que el radio \( OA \), ya que \( BD \cong OA \) por construcción:
$$ \overline{OD} > \overline{OA} $$
De este modo, el punto \( D \) está fuera de la circunferencia.
Por lo tanto, el segmento \( BD \) presenta un punto interior (B) y otro exterior (D), lo cual implica que la intersección se produce únicamente en el punto \( B \).
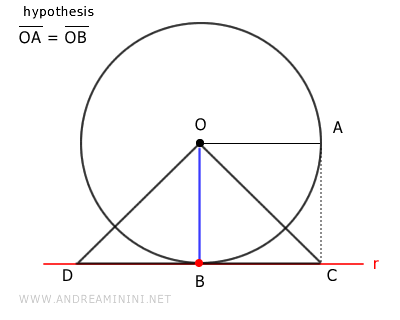
En este caso, el punto de intersección sigue siendo \( B \).
Así, la recta \( r \) corta la circunferencia en un único punto.
Por lo tanto, la recta \( r \) es tangente a la circunferencia.
C] Distancia de la Recta Mayor que el Radio
En este caso, la hipótesis inicial establece que la recta \( r \) se encuentra a una distancia \( OB \) del centro \( O \) de la circunferencia superior al radio \( OA \).
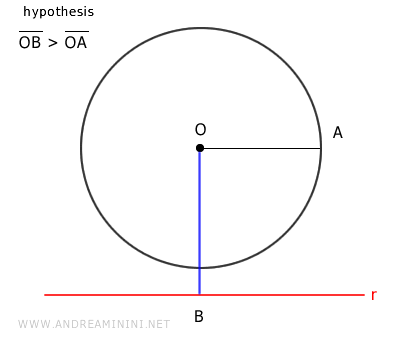
Es decir:
$$ \overline{OB} > \overline{OA} $$
La distancia entre un punto y una recta está representada por el segmento perpendicular más corto que une dicho punto con la recta.
Si esta distancia es mayor que el radio, ningún otro segmento que conecte el centro \( O \) con un punto \( C \) de la recta podrá ser menor.
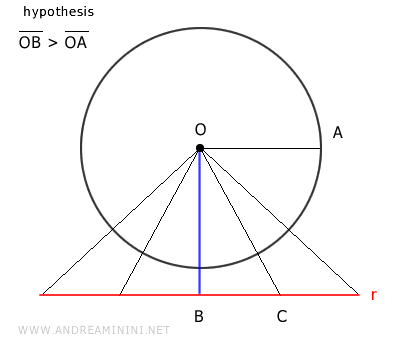
Esto se demuestra fácilmente, ya que cualquier otro punto \( C \) sobre la recta forma un triángulo rectángulo \( OBC \), cuya hipotenusa es el segmento \( OC \).
En un triángulo rectángulo, la hipotenusa siempre es mayor que cualquiera de sus catetos, por lo que OC > OB en todo caso:
$$ \overline{OC} > \overline{OB} $$
Como \( OB > OA \) por hipótesis, se deduce que \( OC \) también es mayor que el radio \( OA \):
$$ \overline{OC} > \overline{OB} > \overline{OA} $$
Por lo tanto, todos los puntos de la recta \( r \) se encuentran fuera de la circunferencia, sin ningún punto en común.
En consecuencia, la recta \( r \) es exterior a la circunferencia.
El Teorema Recíproco
La distancia de una recta al centro de una circunferencia es menor, igual o mayor que el radio si, respectivamente, la recta es secante, tangente o exterior a la circunferencia.
La Demostración
Para demostrar el teorema recíproco, se procede por reducción al absurdo.
Supongamos, para llegar a contradicción, que una recta tangente a una circunferencia no se encuentra a una distancia del centro igual al radio.
Existen dos posibilidades:
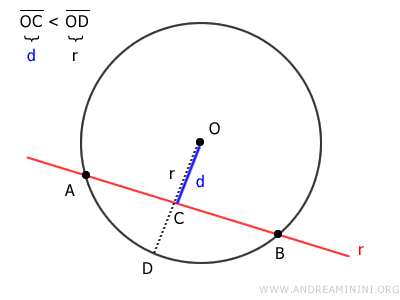
- La distancia es menor que el radio
En tal caso, existirían dos puntos distintos donde la recta intersectaría la circunferencia, lo cual implicaría que es a la vez secante y tangente, lo que es imposible.
- La distancia es mayor que el radio
En este supuesto, la recta no tocaría la circunferencia en ningún punto, lo cual contradice la definición de tangente, que implica un único punto de contacto.
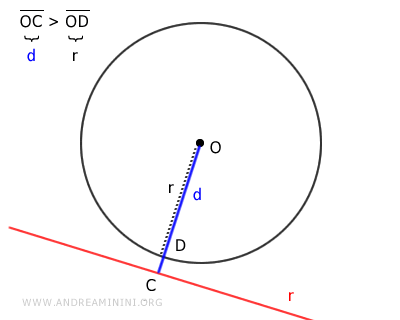
Ambas suposiciones conducen a contradicciones. Por lo tanto, la suposición inicial es falsa y se cumple la proposición contraria.
En conclusión, podemos afirmar con total certeza que una recta tangente se encuentra a una distancia del centro de la circunferencia exactamente igual al radio.
Y así sucesivamente.