Recta Tangente, Secante o Exterior a una Circunferencia
Una recta es tangente a una circunferencia si la corta en un único punto, es exterior si no la corta en absoluto, y es secante si la intersecta en dos puntos.
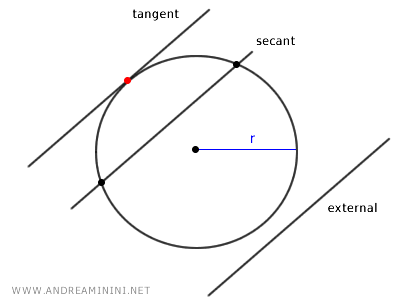
Cómo Determinar si una Recta es Tangente, Secante o Exterior a una Circunferencia
Para saber si una recta es tangente, secante o exterior en geometría analítica, es necesario conocer el radio \( r \) y el centro de la circunferencia \( C(x0, y0) \), así como la ecuación de la recta \( y = mx + q \).
Si una recta es tangente a una circunferencia, la distancia entre ambas coincide exactamente con el valor del radio.
La fórmula para calcular la distancia desde un punto \((x_0, y_0)\) a la recta \( y = mx + q \) es:
$$ d = \frac{|mx_0 - y_0 + q|}{\sqrt{m^2 + 1}} $$
Al comparar el radio con dicha distancia, pueden darse tres situaciones:
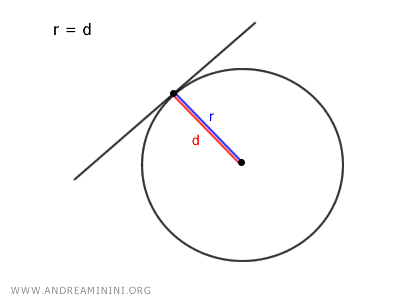
- Si r = d, el radio es igual a la distancia, por lo que la recta es tangente a la circunferencia.
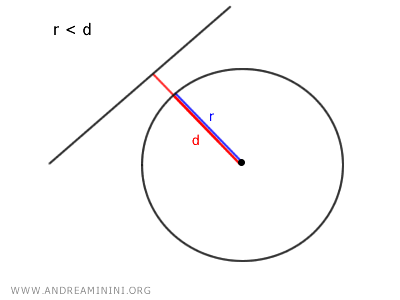
- Si r < d, el radio es menor que la distancia, lo que indica que la recta es exterior a la circunferencia.
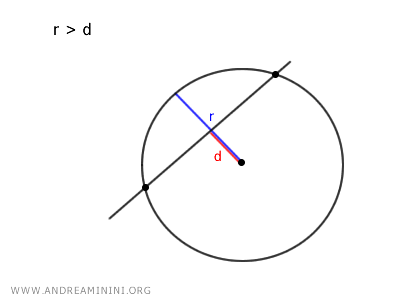
- Si r > d, el radio es mayor que la distancia, lo que significa que la recta es secante y corta a la circunferencia en dos puntos distintos.
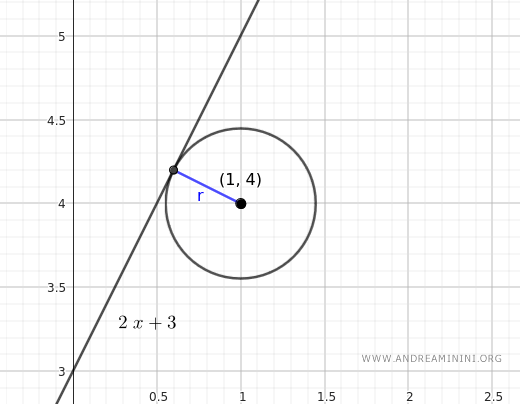
Un Ejemplo Práctico
En este ejemplo, consideremos la ecuación de la recta:
$$ y = 2x + 3 $$
La circunferencia tiene su centro en el punto \( C(1, 4) \) y un radio:
$$ r = \frac{1}{\sqrt{5}} $$
Para determinar si la recta es tangente, secante o exterior a la circunferencia, calculamos la distancia euclídea entre la recta y el centro de la circunferencia.
La fórmula para la distancia \( d \) desde un punto \((x_0, y_0)\) a la recta \( y = mx + q \) es:
$$ d = \frac{|mx_0 - y_0 + q|}{\sqrt{m^2 + 1}} $$
En nuestro caso, la ecuación de la recta es \( y = 2x + 3 \), por lo que \( m = 2 \) y \( q = 3 \).
$$ d = \frac{|2x_0 - y_0 + 3|}{\sqrt{2^2 + 1}} $$
$$ d = \frac{|2x_0 - y_0 + 3|}{\sqrt{4 + 1}} $$
El centro de la circunferencia es \( C(1, 4) \), así que \( x_0 = 1 \) y \( y_0 = 4 \).
$$ d = \frac{|2 \cdot 1 - 4 + 3|}{\sqrt{5}} $$
$$ d = \frac{|2 - 1|}{\sqrt{5}} $$
$$ d = \frac{1}{\sqrt{5}} $$
El radio de la circunferencia y la distancia coinciden, por lo que la recta es tangente a la circunferencia.
$$ r = d = \frac{1}{\sqrt{5}} $$
A continuación, se muestra la representación gráfica del ejercicio:
Y así sucesivamente.