Teorema de Proporcionalidad entre la Secante y la Tangente
Si desde un punto P exterior a una circunferencia se trazan una tangente y una secante, el segmento tangente resulta ser la media proporcional geométrica entre los dos segmentos en que la circunferencia divide a la secante.
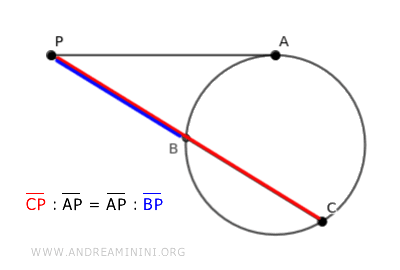
Ejemplo Práctico
Veamos el siguiente caso como ejemplo.
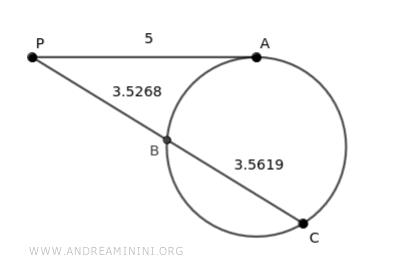
El segmento tangente AP mide 5 unidades.
$$ \overline{AP} = 5 $$
El segmento secante CP es igual a la suma de los segmentos BP y BC:
$$ \overline{CP} = \overline{BP} + \overline{BC} $$
$$ \overline{CP} = 3.5268 + 3.5619 = 7.09 $$
Según el teorema, el segmento CP se relaciona con el segmento tangente AP del mismo modo en que AP se relaciona con BP:
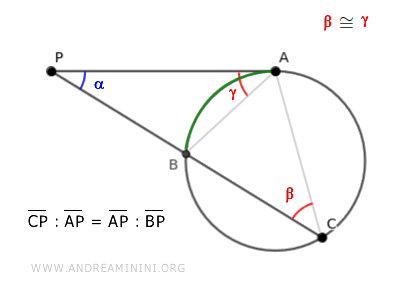
$$ \overline{CP} : \overline{AP} = \overline{AP} : \overline{BP} $$
$$ 7.09 : 5 = 5 : 3.5268 $$
$$ 1.41 = 1.41 $$
Esto confirma la proporción y demuestra que el segmento tangente es, efectivamente, la media geométrica.
Nota. He redondeado los cocientes a dos cifras decimales, ya que las medidas de los segmentos obtenidas con GeoGebra son aproximadas a cuatro decimales.
Demostración
Consideremos una circunferencia y un punto exterior P.
Desde P se trazan una tangente y una secante.
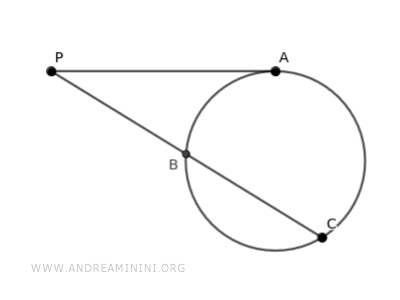
La tangente toca la circunferencia en el punto A, mientras que la secante la corta en los puntos B y C.
Se trazan, además, los segmentos AB y AC.
Así, se forman dos triángulos: ABP y ACP.
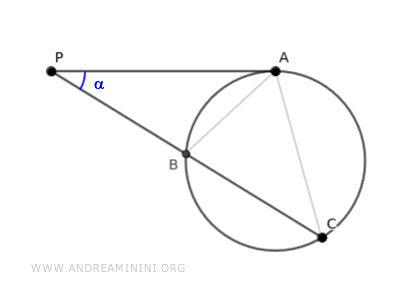
Los triángulos ABP y ACP comparten el mismo ángulo α.
Además, poseen ángulos congruentes β ≅ γ, pues son ángulos inscritos que abarcan el mismo arco AB de la circunferencia.
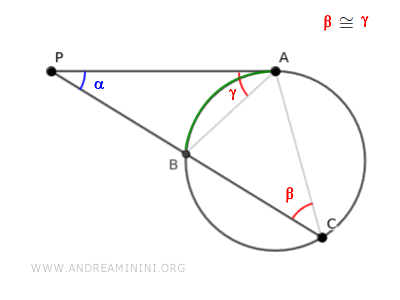
Por lo tanto, según el primer criterio de semejanza de triángulos, los triángulos ABP y ACP son semejantes, pues tienen un ángulo común α y otro par de ángulos congruentes β ≅ γ.
$$ ABP \sim ACP $$
Siendo semejantes, sus lados homólogos son proporcionales:
$$ \overline{AB} : \overline{AC} = \overline{BP} : \overline{AP} = \overline{AP} : \overline{CP} $$
Esto demuestra el teorema:
$$ \overline{BP} : \overline{AP} = \overline{AP} : \overline{CP} $$
Así, el segmento tangente AP es la media proporcional geométrica entre los segmentos de la secante.
Y así sucesivamente.