Longitud de la Circunferencia
La longitud de una circunferencia se puede calcular mediante la fórmula: $$ C = 2\pi r $$
En esta ecuación, \(C\) representa la longitud de la circunferencia, \(\pi\) (Pi) es una constante cuyo valor aproximado es 3.14159, y \(r\) es el radio, es decir, la distancia que hay desde el centro del círculo hasta cualquier punto de su perímetro.
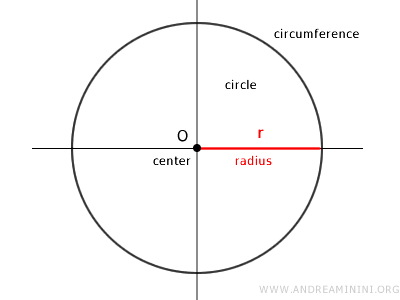
Si tenemos en cuenta que el diámetro \(d = 2r\) equivale al doble del radio, la longitud de la circunferencia también puede expresarse de la siguiente manera:
$$ C = \pi d $$
Esta ecuación demuestra que la razón entre la longitud de la circunferencia (C) y su diámetro (d) es un valor constante conocido como "Pi", independientemente del tamaño del círculo.
$$ \pi = \frac{C}{d} = 3.1415... $$
El descubrimiento de Pi se remonta a la antigüedad, pues ya los egipcios y los babilonios habían intuido su existencia y sus propiedades.
No obstante, fueron los griegos quienes lograron calcular su valor con mayor precisión y rigor matemático.
En definitiva, sin importar el tamaño del círculo que dibujes, la proporción entre su longitud y su diámetro será siempre, aproximadamente, 3.1415... Pi es un número irracional, lo que significa que posee infinitas cifras decimales sin repetirse ni presentar un patrón periódico, aunque suele aproximarse a 3.14 por comodidad en los cálculos.
Y así sucesivamente.