Teorema de los Cuadriláteros Tangenciales

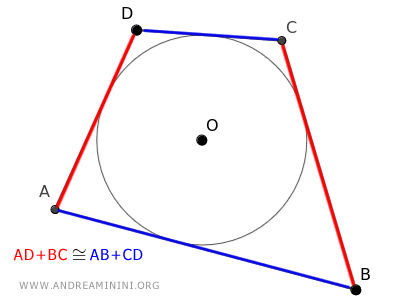
En un cuadrilátero tangencial - es decir, uno circunscrito alrededor de una circunferencia - las sumas de las longitudes de los lados opuestos son iguales: $$ \overline{AB} + \overline{CD} \cong \overline{AD} + \overline{BC} $$. También es cierto el teorema recíproco.

Cuando un cuadrilátero está circunscrito a una circunferencia, cada uno de sus lados es tangente a ella.

En esta figura, la suma de un par de lados opuestos, AD + BC, es igual a la suma del otro par, AB + CD.

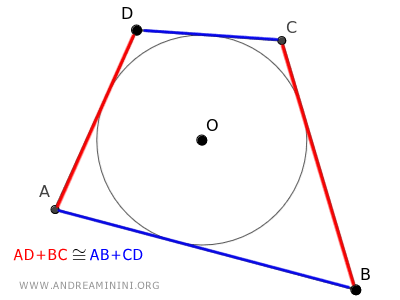
El teorema recíproco también es válido.

Si en un cuadrilátero las sumas de las longitudes de sus lados opuestos son iguales, entonces puede circunscribirse a una circunferencia.

Por tanto, la igualdad entre las sumas de los lados opuestos constituye una condición tanto necesaria como suficiente para que un cuadrilátero sea tangencial.

Demostración

Consideremos un cuadrilátero ABCD circunscrito a una circunferencia de centro O.

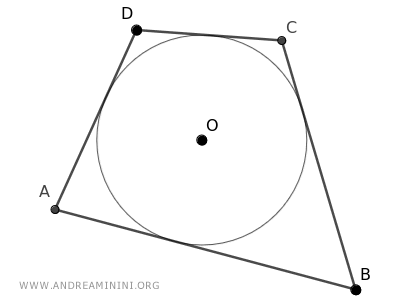
Los puntos donde la circunferencia es tangente a los lados del cuadrilátero se denominan E, F, G y H.

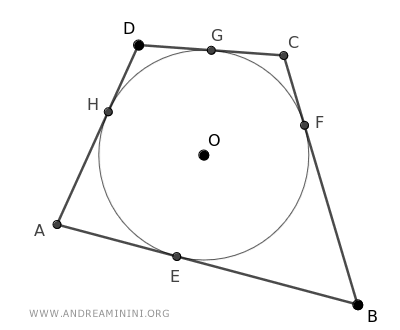
De acuerdo con el Teorema de los Segmentos Tangentes, los segmentos AE ≅ AH son congruentes, ya que el punto A está situado fuera de la circunferencia y es extremo de dos segmentos tangentes.

$$ \overline{AE} \cong \overline{AH} $$

Por el mismo motivo, se cumple que:

$$ \overline{BE} \cong \overline{BF} $$

$$ \overline{CG} \cong \overline{CF} $$

$$ \overline{DG} \cong \overline{DH} $$

Estas congruencias pueden marcarse sobre el cuadrilátero.

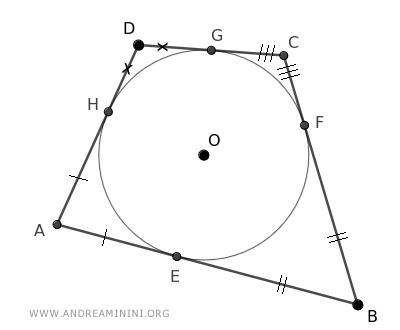
Como la suma de segmentos congruentes también es congruente, podemos sumar los segmentos correspondientes en ambos miembros:

$$ \overline{AE} + \overline{BE} + \overline{CG} + \overline{DG} \cong \overline{AH} + \overline{BF} + \overline{CF} + \overline{DH} $$

Aplicando la propiedad asociativa de la suma, agrupamos los términos del siguiente modo:

$$ (\overline{AE} + \overline{BE}) + (\overline{CG} + \overline{DG}) \cong (\overline{AH} + \overline{DH}) + (\overline{BF} + \overline{CF}) $$

Como AB = AE + BE:

$$ \overline{AB} + (\overline{CG} + \overline{DG}) \cong (\overline{AH} + \overline{DH}) + (\overline{BF} + \overline{CF}) $$

Y dado que CD = CG + DG:

$$ \overline{AB} + \overline{CD} \cong (\overline{AH} + \overline{DH}) + (\overline{BF} + \overline{CF}) $$

Sabiendo que AD = AH + DH:

$$ \overline{AB} + \overline{CD} \cong \overline{AD} + (\overline{BF} + \overline{CF}) $$

Finalmente, como BC = BF + CF:

$$ \overline{AB} + \overline{CD} \cong \overline{AD} + \overline{BC} $$

Así queda demostrado que, en un cuadrilátero tangencial, las sumas de las longitudes de los lados opuestos son iguales.

 

 

Observaciones

A continuación, se presentan algunas observaciones y comentarios adicionales sobre este teorema:

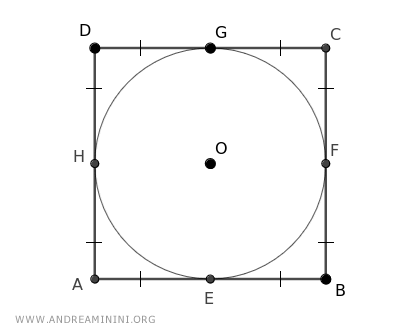
• Tanto el cuadrado como el rombo son ejemplos de cuadriláteros que siempre pueden circunscribirse a una circunferencia.
• En el caso del cuadrado, los puntos de tangencia con la circunferencia coinciden con los puntos medios de sus lados.
  

Y así sucesivamente.