Teorema de los Cuadriláteros Cíclicos
En un cuadrilátero cíclico - es decir, inscrito en una circunferencia - los ángulos opuestos son suplementarios, y también se cumple el recíproco.
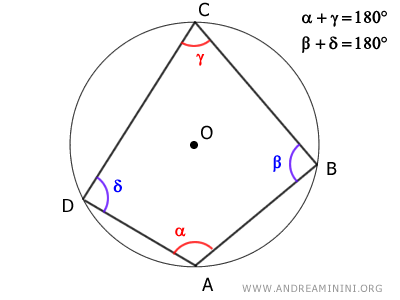
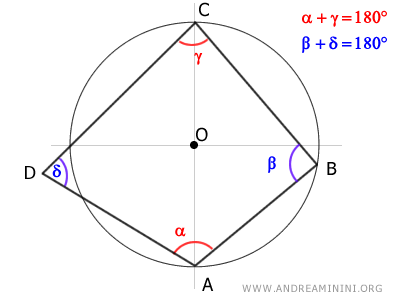
Cuando un cuadrilátero está inscrito en una circunferencia, sus ángulos opuestos son suplementarios; es decir, suman un ángulo llano de 180°.
$$ \alpha + \gamma \cong 180° $$
$$ \beta + \delta \cong 180° $$
El recíproco de este teorema también es válido.
Si un cuadrilátero tiene ángulos opuestos suplementarios, entonces puede inscribirse en una circunferencia.
Por tanto, tener ángulos opuestos suplementarios constituye tanto una condición necesaria como suficiente para que un cuadrilátero sea cíclico.
Demostración
Vamos a analizar un cuadrilátero inscrito en una circunferencia.
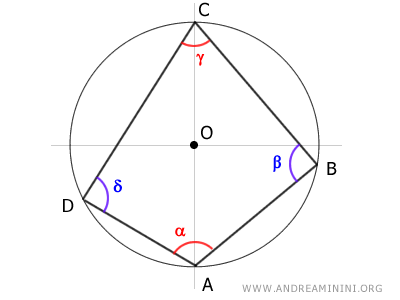
Se trazan los radios OB y OD, que dividen el ángulo completo en el centro en dos ángulos centrales, α' y γ'.
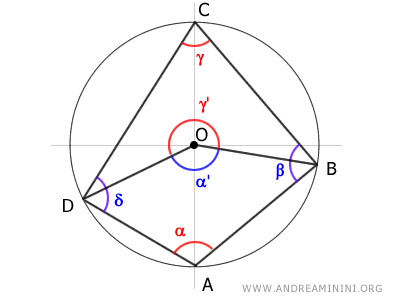
Es importante destacar que la suma de estos dos ángulos centrales equivale a una vuelta completa (360°), dato fundamental para lo que sigue.
$$ \alpha' + \gamma' = 360° $$
El ángulo α es un ángulo inscrito que abarca el arco BCD.
De acuerdo con el Teorema de los Ángulos Centrales e Inscritos, un ángulo inscrito α mide la mitad del ángulo central γ' que abarca el mismo arco BCD.
$$ \alpha = \frac{1}{2} \cdot \gamma' $$
$$ \gamma' = 2 \cdot \alpha $$
De modo similar, el ángulo γ es un ángulo inscrito que abarca el arco BAD.
Otra vez, según el Teorema de los Ángulos Centrales e Inscritos, el ángulo inscrito γ mide la mitad del ángulo central α' que abarca el mismo arco BAD.
$$ \gamma = \frac{1}{2} \cdot \alpha' $$
$$ \alpha' = 2 \cdot \gamma $$
Como sabemos que la suma de los ángulos centrales es una vuelta completa:
$$ \alpha' + \gamma' = 360° $$
Si sustituimos α' = 2γ y γ' = 2α, obtenemos:
$$ 2 \cdot \gamma + 2 \cdot \alpha = 360° $$
Dividimos ambos términos de la ecuación entre dos, y queda:
$$ \frac{2 \cdot \gamma + 2 \cdot \alpha}{2} = \frac{360°}{2} $$
$$ \gamma + \alpha = 180° $$
Así, hemos demostrado que la suma de los ángulos opuestos α y γ en el cuadrilátero es 180°.
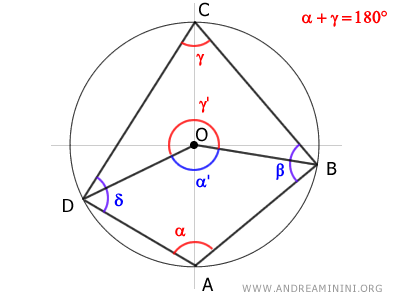
Una vez demostrado que los ángulos opuestos α y γ son suplementarios (α + γ = 180°), es fácil deducir que el otro par de ángulos opuestos también lo es.
Podríamos repetir el mismo razonamiento, esta vez trazando los radios OA y OC y analizando los ángulos β y δ de manera análoga.
No obstante, resulta mucho más eficiente recordar que la suma de los ángulos interiores de cualquier cuadrilátero es siempre 360°.
$$ \alpha + \beta + \gamma + \delta = 360° $$
Si aplicamos la propiedad asociativa, podemos reagrupar los términos así:
$$ (\alpha + \gamma) + (\beta + \delta) = 360° $$
Como ya sabemos que un par de ángulos opuestos suma 180°:
$$ 180° + (\beta + \delta) = 360° $$
$$ \beta + \delta = 360° - 180° $$
$$ \beta + \delta = 180° $$
Por tanto, el otro par de ángulos opuestos, β y δ, también suma 180°.
Queda así demostrada la propiedad de que en todo cuadrilátero cíclico, ambos pares de ángulos opuestos son suplementarios.
Demostración del Teorema Recíproco
En este caso, partimos de un conjunto distinto de hipótesis.
Consideremos un cuadrilátero ABCD
cuyos ángulos opuestos sean suplementarios.
$$ \alpha + \gamma = 180° $$
$$ \beta + \delta = 180° $$
Queremos demostrar que dicho cuadrilátero se puede inscribir en una circunferencia.
Para probarlo, empleamos una demostración por reducción al absurdo. Supongamos, en cambio, que «el cuadrilátero no es cíclico porque la circunferencia no pasa por uno de sus vértices».
Supongamos, por ejemplo, que la circunferencia no pasa por el punto D.
Dado que por tres puntos cualesquiera siempre es posible trazar una circunferencia, existe sin duda una circunferencia que pase por los vértices A, B y C del cuadrilátero.
En tal caso, el punto D estará o bien en el interior o bien en el exterior de dicha circunferencia.
Analicemos ambos supuestos:
A] El vértice D está fuera de la circunferencia
Aquí, el vértice D se encuentra fuera de la circunferencia.
Como el vértice C está sobre la circunferencia, el segmento CD intersecta necesariamente la circunferencia en un punto intermedio E.
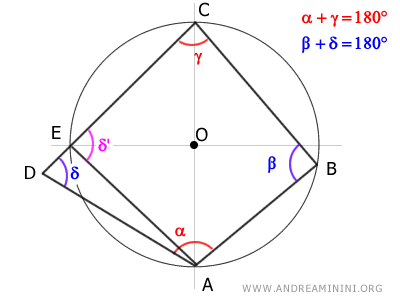
Según nuestra hipótesis inicial, el cuadrilátero ABCD es cíclico y, por tanto, presenta ángulos opuestos suplementarios.
Concretamente, se cumple que β + δ = 180°.
$$ \beta + \delta = 180° $$
Sin embargo, los ángulos β y δ' también son ángulos opuestos en el cuadrilátero AECD, por lo que también deben sumar 180°: β + δ' = 180°.
$$ \beta + \delta' = 180° $$
De aquí se deduce que los ángulos δ y δ' son congruentes, ya que ambos son suplementarios al mismo ángulo β.
Además, los ángulos δ y δ' son ángulos correspondientes formados por las rectas AD y AE, cortadas por la transversal DE.
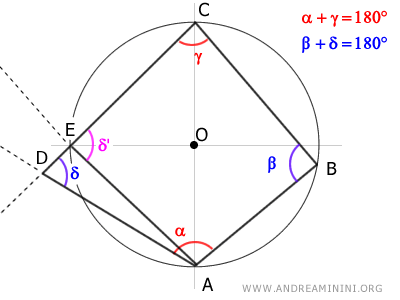
Por el Teorema de las Rectas Paralelas, si los ángulos correspondientes δ y δ' son congruentes, entonces las rectas AD y AE deberían ser paralelas.
Pero esto es imposible, ya que los segmentos AD y AE comparten el punto A, y por tanto, pertenecen a rectas secantes y no paralelas.
Así, nuestra suposición inicial resulta falsa.
B] El vértice D está dentro de la circunferencia
En este caso, el vértice D está situado en el interior de la circunferencia.
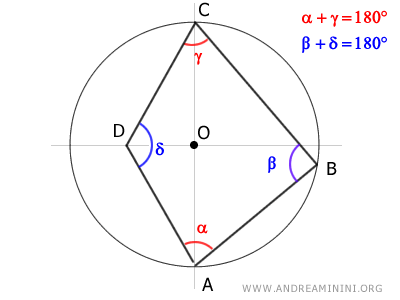
Como el vértice C está sobre la circunferencia, prolongar el segmento CD lo hace intersectar la circunferencia en un punto E.
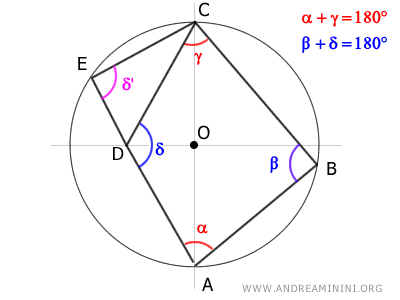
Nuevamente, según nuestra hipótesis inicial, el cuadrilátero ABCD es cíclico y, por tanto, presenta ángulos opuestos suplementarios.
En concreto, β + δ = 180°.
$$ \beta + \delta = 180° $$
No obstante, los ángulos β y δ' también son opuestos en el cuadrilátero AECD, y por tanto, son suplementarios: β + δ' = 180°.
$$ \beta + \delta' = 180° $$
Por lo tanto, los ángulos δ y δ' resultan congruentes, pues ambos son suplementarios al mismo ángulo β.
Además, los ángulos δ y δ' son ángulos correspondientes formados por las rectas CD y CE, cortadas por la transversal DE.
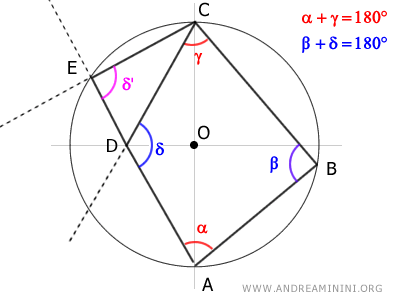
Por el Teorema de las Rectas Paralelas, si los ángulos correspondientes δ y δ' son congruentes, entonces las rectas CD y CE tendrían que ser paralelas.
Pero esto contradice el hecho de que los segmentos CD y CE comparten el punto C y, por tanto, están sobre rectas secantes.
Así que, nuevamente, nuestra suposición inicial es falsa.
En conclusión, la suposición inicial es falsa tanto si el punto D está fuera como si está dentro de la circunferencia.
Por consiguiente, se impone lo contrario: el punto D debe estar sobre la circunferencia.
Esto demuestra que «un cuadrilátero puede inscribirse en una circunferencia si y solo si dicha circunferencia pasa por sus cuatro vértices».
Observaciones
Aquí tienes algunas notas y observaciones adicionales:
- Un cuadrilátero convexo puede inscribirse en una circunferencia si la suma de sus pares de ángulos opuestos es igual: $$ \alpha + \gamma \cong \beta + \delta $$ pues ambas suman un ángulo llano (180°).
- Todo rectángulo, cuadrado y trapecio isósceles puede inscribirse en una circunferencia, ya que en todas estas figuras los ángulos opuestos son siempre suplementarios.
Y así sucesivamente.