Geometría Analítica
La geometría analítica, también conocida como geometría cartesiana, es una rama de las matemáticas que utiliza herramientas algebraicas para representar y resolver problemas de índole geométrica.
En esencia, la geometría analítica establece un vínculo entre las figuras geométricas y las expresiones algebraicas que las describen.
¿En qué se diferencia de la geometría euclidiana?
La geometría euclidiana se fundamenta en axiomas y construcciones geométricas abstractas, como los postulados de Euclides.
Por el contrario, la geometría analítica emplea coordenadas \((x;y)\) o \((x;y;z)\) y el álgebra para representar objetos geométricos (como puntos, rectas, curvas, planos o sólidos) y resolver problemas tanto en el plano como en el espacio tridimensional.
Entre los conceptos fundamentales de la geometría analítica se encuentran:
- Ecuaciones
Las figuras geométricas se expresan mediante ecuaciones. Por ejemplo, una recta en el plano puede representarse por una ecuación lineal de dos variables \( ax + by + c = 0 \), mientras que una circunferencia se describe con una ecuación cuadrática \( x^2 + y^2 = r^2 \), donde \( r \) es el radio. Ecuaciones más complejas permiten describir curvas (como parábolas, hipérbolas o elipses) o superficies en el espacio tridimensional. - Sistema de Coordenadas
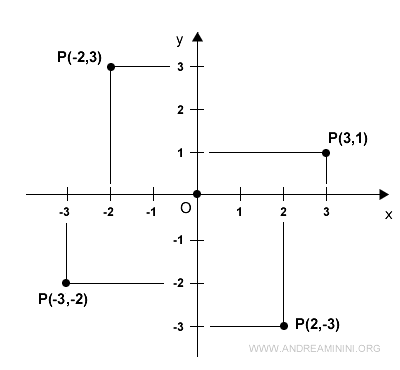
El sistema más utilizado es el sistema de coordenadas cartesianas, o el plano cartesiano, que se basa en dos o tres ejes perpendiculares para definir la posición de un punto en el plano (2D) o en el espacio (3D). Cada punto se identifica mediante un par o un trío de números denominados coordenadas \((x;y)\) o \((x;y;z)\), que determinan su localización respecto a los ejes.
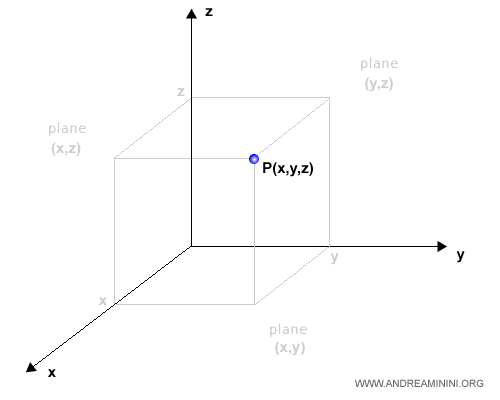
En el espacio tridimensional, las coordenadas de un punto se expresan mediante un trío de valores \((x;y;z)\), que indican su posición relativa a los tres ejes.
Uno de los objetivos esenciales de la geometría analítica es determinar los puntos de intersección entre curvas (o superficies), lo que se traduce en la resolución de sistemas de ecuaciones.
Asimismo, permite calcular distancias entre dos puntos o el ángulo formado entre dos rectas, a partir de las coordenadas de los puntos y de las ecuaciones de las rectas implicadas.
Origen e Historia de la Geometría Analítica. La geometría analítica surgió en el siglo XVII de la mano de René Descartes (conocido en italiano como “Cartesio”) y Pierre de Fermat, marcando un hito fundamental en la historia de las matemáticas. Su aparición permitió integrar de forma inédita el álgebra y la geometría, razón por la cual también se la denomina "geometría cartesiana". Este enfoque sentó las bases para avances trascendentales en múltiples áreas, como el cálculo diferencial e integral, la mecánica clásica y la teoría de la relatividad.
Ejemplo Práctico
Veamos cómo hallar el punto de intersección entre dos rectas en el plano cartesiano.
Las rectas están definidas por las siguientes ecuaciones:
$$ L_1: y = 2x + 1 $$
$$ L_2: y = -x + 5 $$
Para encontrar el punto de intersección, debemos determinar los valores de \( x \) y \( y \) que satisfacen simultáneamente ambas ecuaciones.
Esto implica resolver el sistema de ecuaciones lineales formado por dichas rectas.
Planteamos el sistema y despejamos \( x \) y \( y \):
$$ \begin{cases} y = 2x + 1 \\ y = -x + 5 \end{cases} $$
$$ \begin{cases} -x + 5 = 2x + 1 \\ y = -x + 5 \end{cases} $$
$$ \begin{cases} -x - 2x = -5 + 1 \\ y = -x + 5 \end{cases} $$
$$ \begin{cases} -3x = -4 \\ y = -x + 5 \end{cases} $$
$$ \begin{cases} x = \frac{4}{3} \\ y = -x + 5 \end{cases} $$
Sustituimos \( x = \frac{4}{3} \) en la otra ecuación para hallar \( y \):
$$ \begin{cases} x = \frac{4}{3} \\ y = -\left( \frac{4}{3} \right) + 5 \end{cases} $$
$$ \begin{cases} x = \frac{4}{3} \\ y = \frac{-4 + 15}{3} \end{cases} $$
$$ \begin{cases} x = \frac{4}{3} \\ y = \frac{11}{3} \end{cases} $$
$$ \begin{cases} x = 1.3333 \\ y = 3.6667 \end{cases} $$
Por lo tanto, el punto de intersección de las rectas \( L_1 \) y \( L_2 \) es \(\left(1.3333, 3.6667 \right)\).
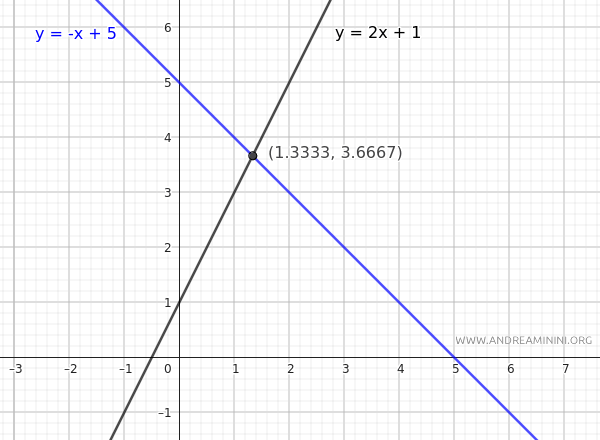
Este ejemplo demuestra cómo la geometría analítica permite resolver problemas geométricos de manera precisa utilizando herramientas algebraicas, sin depender exclusivamente de representaciones gráficas.
Y así sucesivamente.