Ecuación de la Bisectriz de un Ángulo

La bisectriz de un ángulo es la semirrecta que parte del vértice y divide el ángulo en dos partes iguales. La ecuación de la bisectriz se expresa así:

$$ \frac{ax+by+c}{ \sqrt{a^2+b^2}} = \pm \frac{a'x+b'y+c'}{ \sqrt{a'^2+b'^2}} $$

Esta ecuación determina las dos bisectrices que dividen un ángulo en dos ángulos congruentes.

El signo ± indica que existen dos bisectrices: una correspondiente al ángulo agudo y otra al ángulo obtuso que se forman en la intersección de las dos rectas.

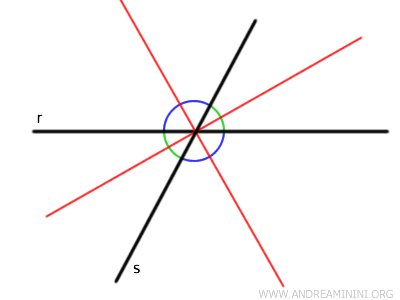
Nota: Esta fórmula se basa en que los puntos que se encuentran sobre la bisectriz están a igual distancia de las dos rectas. La bisectriz constituye el lugar geométrico de los puntos equidistantes a ambos lados del ángulo.

Ejemplo Práctico

Consideremos las ecuaciones de dos rectas no paralelas:

$$ r : 3x+4y-6=0 $$

$$ s: 4x-3y-4=0 $$

Estas dos rectas se intersectan, formando dos pares de ángulos opuestos y congruentes: un par de ángulos agudos y otro par de ángulos obtusos.

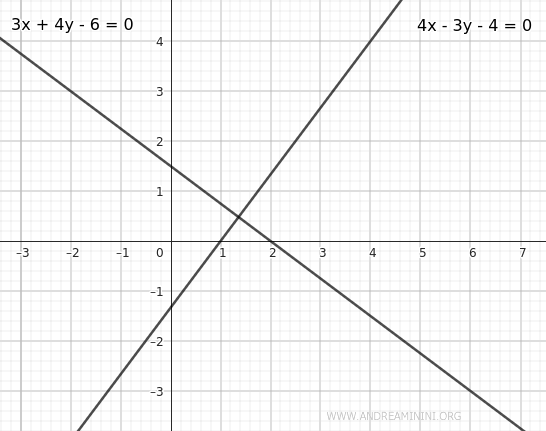
Para hallar las ecuaciones de las dos bisectrices, empleamos la siguiente fórmula:

$$ \frac{ax+by+c}{ \sqrt{a^2+b^2}} = \pm \frac{a'x+b'y+c'}{ \sqrt{a'^2+b'^2}} $$

Sustituyamos los coeficientes de las rectas r y s: a=3, b=4, c=-6 y a'=4, b'=-3, c'=-4.

$$ \frac{3x+4y-6}{ \sqrt{3^2+4^2}} = \pm \frac{4x-3y-4}{ \sqrt{4^2+(-3)^2}} $$

$$ \frac{3x+4y-6}{ \sqrt{9+16}} = \pm \frac{4x-3y-4}{ \sqrt{16+9}} $$

$$ \frac{3x+4y-6}{ \sqrt{25}} = \pm \frac{4x-3y-4}{ \sqrt{25}} $$

$$ \frac{3x+4y-6}{ 5 } = \pm \frac{4x-3y-4}{ 5} $$

Multiplicamos ambos lados por 5 para simplificar:

$$ \frac{3x+4y-6}{ 5 } \cdot 5 = \pm \frac{4x-3y-4}{ 5} \cdot 5 $$

$$ 3x+4y-6 = \pm (4x-3y-4) $$

Consideremos ambos casos según el signo:

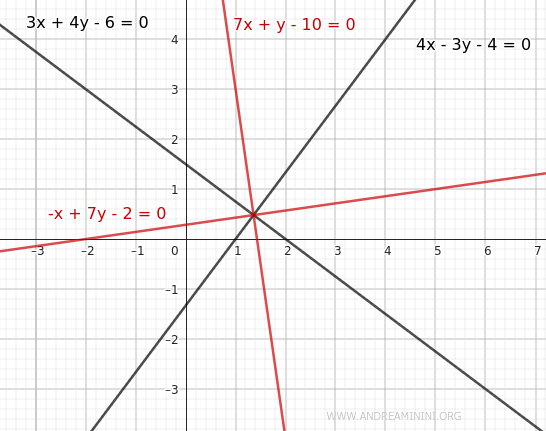
• Primer caso (+): $$ 3x+4y-6 = 4x-3y-4 $$ $$ 3x+4y-6 - 4x + 3y + 4 = 0 $$ Simplificando, obtenemos la ecuación de una bisectriz: $$ -x+7y-2 = 0 $$
• Segundo caso (-): $$ 3x+4y-6 = -(4x-3y-4) $$ $$ 3x+4y-6 = -4x+3y+4 $$ $$ 3x+4y-6 + 4x - 3y -4 = 0 $$ Lo que conduce a la ecuación de la otra bisectriz: $$ 7x+y-10 = 0 $$

Así, obtenemos las ecuaciones de las bisectrices correspondientes a los dos pares de ángulos opuestos.

La Demostración

Un ángulo se forma entre dos semirrectas r y s, denominadas “lados” del ángulo, que parten de un mismo punto llamado “vértice”.

Consideremos las ecuaciones de las dos rectas:

$$ r: \ ax+by+c=0 $$

$$ s: \ a'x+b'y+c'=0 $$

La bisectriz de un ángulo es una semirrecta que parte del vértice y se caracteriza porque cualquier punto situado sobre ella está a la misma distancia de los lados del ángulo.

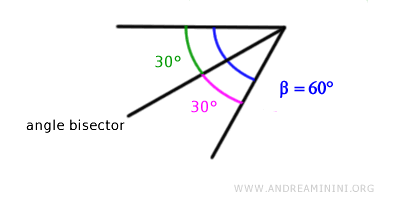
Por lo tanto, la bisectriz constituye el lugar geométrico de los puntos equidistantes a los lados del ángulo.

Por ejemplo, si elegimos un punto P sobre la bisectriz, la distancia de P a la recta r se mide mediante el segmento $ \overline{AP} $, perpendicular a r, cuyo extremo está en P y otro punto A sobre r. De forma análoga, la distancia de P a la recta s es el segmento $ \overline{BP} $.

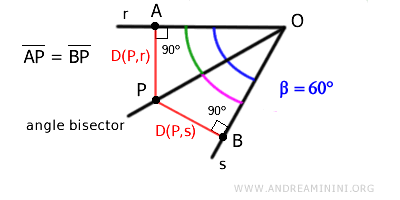
El punto P está equidistante de ambas rectas si, y solo si, los segmentos $ \overline{AP} \cong \overline{BP} $ son congruentes, es decir, tienen la misma longitud.

$$ \overline{AP} \cong \overline{BP} $$

Por tanto, los puntos equidistantes cumplen la ecuación:

$$ D(P,r) = D(P,s) $$

La fórmula que calcula la distancia D(P,r) de un punto P(x;y) a la recta r es:

$$ D(P,r) = \frac{|ax+by+c|}{ \sqrt{a^2+b^2}} $$

Y la fórmula para la distancia D(P,s) a la recta s es:

$$ D(P,s) =\frac{|a'x+b'y+c'|}{ \sqrt{a'^2+b'^2}} $$

Nota: Es fundamental recordar que las distancias se expresan en valor absoluto, ya que representan longitudes y, por tanto, siempre son valores no negativos.

Al sustituir las fórmulas de las distancias D(P,r) y D(P,s) en la igualdad, obtenemos:

$$ D(P,r)=D(P,s) $$

$$ \frac{|ax+by+c|}{ \sqrt{a^2+b^2}} = \frac{|a'x+b'y+c'|}{ \sqrt{a'^2+b'^2}} $$

Sin embargo, el razonamiento no está completo, ya que cuando dos rectas se cortan, generan cuatro ángulos, es decir, dos pares de ángulos opuestos y congruentes.

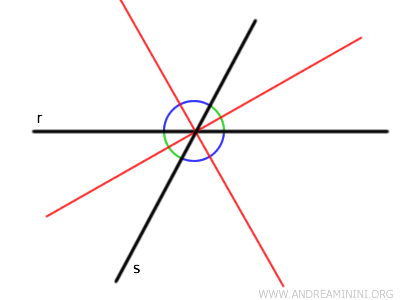
Por tanto, las bisectrices a considerar son dos rectas perpendiculares entre sí. Una divide el ángulo agudo, mientras que la otra divide el ángulo obtuso.

Para encontrar ambas ecuaciones de bisectrices, eliminamos el valor absoluto en el primer miembro de la ecuación y consideramos ambos signos en el segundo miembro:

$$ \frac{ax+by+c}{ \sqrt{a^2+b^2}} = \pm \frac{a'x+b'y+c'}{ \sqrt{a'^2+b'^2}} $$

Esto concluye la demostración de la fórmula de la ecuación de las bisectrices de los ángulos formados por dos rectas.

Y así sucesivamente.