Volumen de un Prisma Rectangular
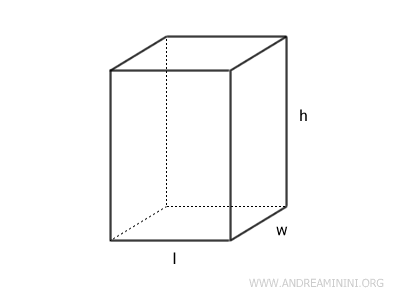
El volumen V de un prisma rectangular se calcula multiplicando el área de su base AB por su altura h: $$ V = A_B \cdot h $$ Alternativamente, dado que $ A_B = l \cdot w $, el volumen puede expresarse como el producto de la longitud (l), el ancho (w) y la altura (h) del prisma: $$ V = l \cdot w \cdot h $$
Demostración
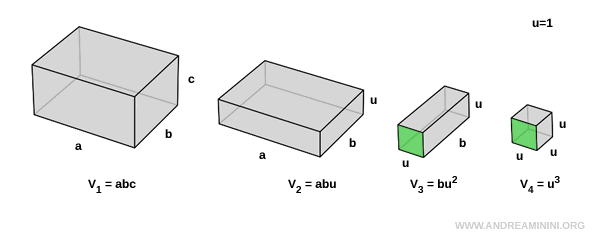
Consideremos cuatro prismas rectangulares y supongamos que la unidad de medida es $ u = 1 $.
El sólido final es un cubo unitario cuyo volumen es $ V_4 = u^3 $.
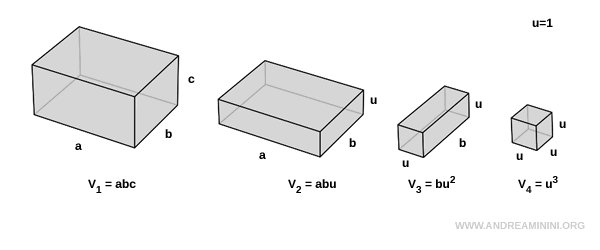
Queremos demostrar que el volumen del primer prisma está dado por $ V_1 = abc $.
Utilizaremos un razonamiento constructivo. Partimos de un cubo unitario y observamos que el volumen de cualquier sólido puede determinarse contando cuántos cubos unitarios ($ u = 1 $) lo componen.
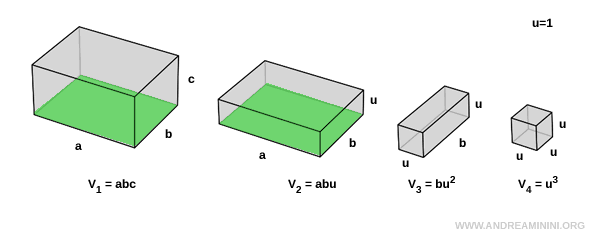
El primer y el segundo prisma comparten la misma área de base $ a \cdot b $, pero tienen alturas distintas ( $ c $ en el primero y $ u $ en el segundo):
$$ V_1 = a \cdot b \cdot c $$
$$ V_2 = a \cdot b \cdot u $$
De acuerdo con una propiedad de los prismas, si las bases son iguales, sus volúmenes son proporcionales a sus alturas:
$$ V_1 : V_2 = c : u $$
De ahí se deduce:
$$ V_1 = \frac{c}{u} \cdot V_2 $$
Como $ u = 1 $, se simplifica a:
$$ V_1 = c \cdot V_2 $$
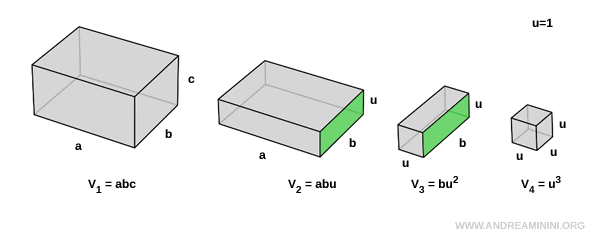
El segundo y el tercer prisma tienen en común una cara de área $ b \cdot u $, pero difieren en longitud ( $ a $ frente a $ u $ ):
$$ V_2 = a \cdot b \cdot u $$
$$ V_3 = u \cdot b \cdot u $$
En este caso, sus volúmenes son proporcionales a sus longitudes:
$$ V_2 : V_3 = a : u $$
Por tanto:
$$ V_2 = \frac{a}{u} \cdot V_3 = a \cdot V_3 $$
Analicemos ahora el tercer y el cuarto prisma. Comparten una cara de área $ u \cdot u $, pero difieren en ancho ( $ b $ frente a $ u $ ):
$$ V_3 = u \cdot b \cdot u $$
$$ V_4 = u \cdot u \cdot u $$
También en este caso, sus volúmenes guardan proporción:
$$ V_3 : V_4 = b : u $$
Por consiguiente:
$$ V_3 = \frac{b}{u} \cdot V_4 = b \cdot V_4 $$
Volviendo al primer prisma, podemos expresar su volumen en función de los otros prismas:
$$ V_1 = c \cdot V_2 $$
Como $ V_2 = a \cdot V_3 $, tenemos:
$$ V_1 = c \cdot (a \cdot V_3) $$
Y dado que $ V_3 = b \cdot V_4 $, se obtiene:
$$ V_1 = c \cdot (a \cdot (b \cdot V_4)) $$
Esto demuestra que el primer prisma está formado por $ a \cdot b \cdot c $ cubos unitarios de volumen $ V_4 $:
$$ V_1 = a \cdot b \cdot c \cdot V_4 $$
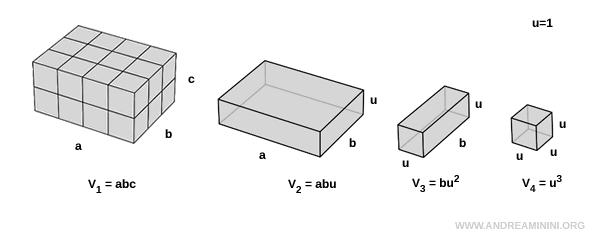
Dado que $ V_4 = u^3 = 1 $, la expresión final se simplifica a:
$$ V_1 = a \cdot b \cdot c $$
Queda así demostrado que el volumen de un prisma rectangular es, en efecto, el producto de su longitud, ancho y altura.
Y así sucesivamente.