Secciones Paralelas de un Ángulo Diedro
En un ángulo diedro, las secciones paralelas son siempre congruentes.
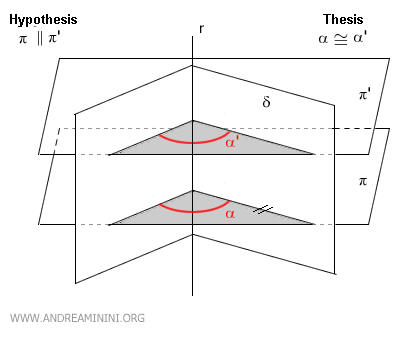
Por ejemplo, sea el plano π que corta el ángulo diedro y forma un ángulo α.
Si consideramos otro plano π' paralelo a π (es decir, π || π'), este también intersecta el ángulo diedro, generando un ángulo congruente α ≅ α'.
Como el ángulo diedro es el mismo, ambas secciones paralelas resultan necesariamente congruentes.
Demostración
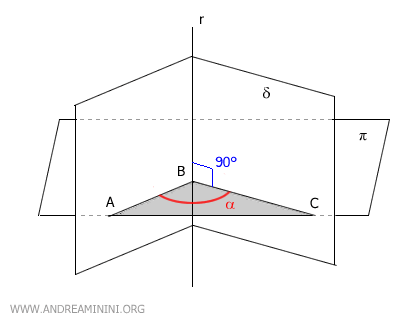
Consideremos el ángulo diedro δ y un plano π que lo corta a lo largo de la arista r (es decir, constituye una sección normal).
Para simplificar, supongamos que dicho plano es perpendicular a la arista (90°), aunque el razonamiento sería válido para cualquier otra inclinación.
El plano π intersecta el ángulo diedro δ en los puntos A, B y C.
Ahora, consideremos un segundo plano π', paralelo a π.
Este plano π' corta el ángulo diedro en los puntos A', B' y C'.

Como ambos planos son paralelos, los cuadriláteros AA'B'B y BB'C'C resultan ser paralelogramos.
En un paralelogramo, los lados opuestos son congruentes. De esto se deduce que AA' ≅ BB', AB ≅ A'B', BB' ≅ CC' y BC ≅ B'C'.
Además, gracias a la propiedad transitiva, si AA' ≅ BB' y BB' ≅ CC', podemos concluir que AA' ≅ CC'.

Una vez establecido que los segmentos AA' ≅ CC' son congruentes, se deduce que el cuadrilátero AA'C'C también es un paralelogramo.
Por lo tanto, los lados inclinados de ese paralelogramo, AC ≅ A'C', son congruentes.

En este punto, se observa que los triángulos ABC y A'B'C' son congruentes según el criterio de congruencia Lado-Lado-Lado (LLL), ya que tienen sus tres lados correspondientes congruentes: AC ≅ A'C', AB ≅ A'B' y BC ≅ B'C'.

Dado que ambos triángulos son congruentes, sus ángulos correspondientes también lo son.
En particular, los ángulos α ≅ α' son congruentes, lo que demuestra que las secciones paralelas del ángulo diedro δ son congruentes.
$$ \alpha \cong \alpha' $$
Así queda demostrado el teorema.
Y así sucesivamente.