Cadenas Poligonales
En geometría, una cadena poligonal (o línea poligonal) es una sucesión de segmentos rectos enlazados uno tras otro para formar una cadena o una red. A estos segmentos se los denomina habitualmente lados, y a sus extremos, vértices.
En una línea poligonal, cada vértice puede estar conectado, como máximo, a dos segmentos.
Las cadenas poligonales pueden clasificarse en abiertas, cerradas o entrecruzadas.
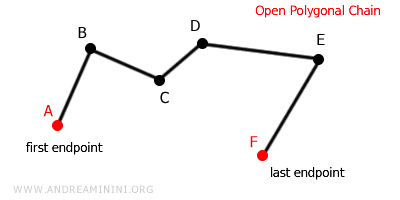
- Cadenas Poligonales Abiertas
En las cadenas poligonales abiertas, el último extremo no se une nuevamente con el primero.
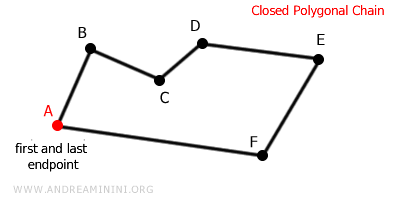
- Cadenas Poligonales Cerradas
En las cadenas poligonales cerradas, el último tramo se enlaza de nuevo con el primer vértice.
Las cadenas poligonales cerradas conforman figuras conocidas como polígonos, que pueden adoptar múltiples formas. Estos pueden ser regulares, si todos sus lados y ángulos son iguales, o irregulares, cuando presentan lados o ángulos desiguales. - Cadenas Poligonales Entrecruzadas
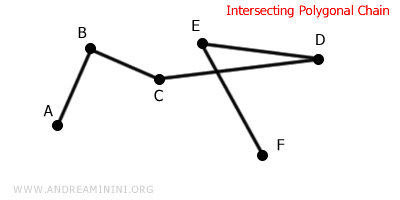
En las cadenas poligonales entrecruzadas, al menos dos lados no consecutivos se cruzan entre sí.
Aplicaciones Prácticas de las Cadenas Poligonales. En topografía, las cadenas poligonales se construyen a partir de puntos medidos con gran precisión y permiten determinar la posición relativa de distintos puntos sobre la superficie terrestre. Esta técnica resulta fundamental en la elaboración de mapas y en los trabajos de mensura de terrenos. Además, las cadenas poligonales se utilizan ampliamente en el ámbito de los gráficos por computadora para modelar formas tridimensionales. Por ejemplo, en los videojuegos y en la animación digital, los objetos 3D suelen representarse mediante una red de polígonos, donde cada polígono representa una porción de la superficie del objeto. A este método se lo conoce como modelado poligonal.
Y así sucesivamente.