Longitud
Longitud es la medida que expresa la extensión espacial de un objeto. Por ejemplo, la longitud de un segmento de recta.
La longitud es una de las magnitudes físicas fundamentales, ya que no se define a partir de ninguna otra magnitud física.
En el Sistema Internacional de Unidades (SI), la unidad de medida de longitud es el metro, junto con sus múltiplos (como el kilómetro) y sus submúltiplos (como el centímetro, milímetro, etc.).
De acuerdo con la definición vigente, un metro es la distancia que recorre la luz en el vacío en 1/299.792.458 de segundo.
Nota: La historia de la medición de la longitud se remonta a las civilizaciones antiguas, debido a sus múltiples aplicaciones prácticas (como la construcción de edificaciones o la medición de rutas comerciales, entre otras). En la Antigüedad, las unidades de medida se basaban en partes del cuerpo humano, como el pie o el antebrazo. Por ejemplo, el codo egipcio correspondía a la distancia entre la mano y el codo. Con los avances tecnológicos y científicos, estas medidas se estandarizaron para facilitar el comercio y la comunicación científica.
El significado de la longitud
La longitud es una de las magnitudes más esenciales para comprender y describir nuestro entorno.
Por ejemplo, basta con un vistazo rápido para saber si un palo es más largo o más corto que otro.

No obstante, detrás de la aparente sencillez de la palabra "longitud" se esconde una gran complejidad, pues su significado puede variar según el contexto, el área de estudio o la disciplina técnica o científica.
Por ejemplo, en geometría euclidiana, la longitud de un segmento se define simplemente como la distancia entre sus dos extremos.

Dos segmentos se consideran congruentes si poseen la misma longitud, es decir, si pueden superponerse ocupando exactamente los mismos puntos en el plano.
En tales casos, se dice que ambos segmentos congruentes pertenecen a la misma clase de equivalencia.

Por su parte, la longitud de una línea poligonal se obtiene sumando las longitudes de cada uno de sus segmentos.

En geometría sólida, la longitud es una de las tres dimensiones, junto con la altura y la profundidad (o anchura), necesarias para determinar el tamaño de un objeto.

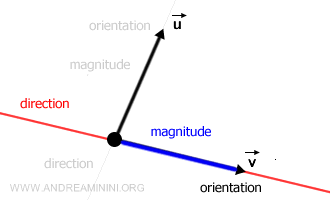
En álgebra lineal, longitud (o magnitud) hace referencia al módulo de un vector, y es equivalente a su norma o valor absoluto.
Un vector suele representarse mediante una flecha, y el módulo del vector se corresponde con la longitud de dicha flecha.
En física, la longitud es una magnitud física fundamental, que se mide en metros y se simboliza con [L] en el análisis dimensional.
Por eso, comprender qué significa “longitud” requiere tener siempre presente el contexto en el que se emplea.
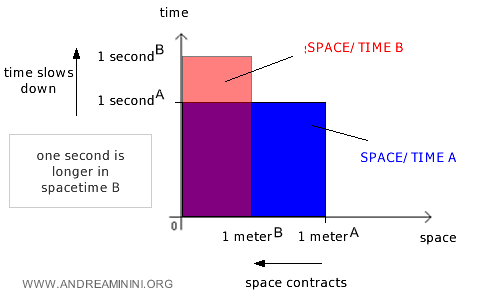
Nota: En el contexto de la teoría de la relatividad especial de Einstein, la cuestión se vuelve aún más compleja, ya que la longitud deja de ser una medida absoluta y pasa a convertirse en una magnitud relativa. Por ejemplo, la longitud de un objeto en movimiento resulta más corta que la medida realizada por un observador en reposo, fenómeno conocido como contracción de la longitud. Este efecto se manifiesta a velocidades cercanas a la de la luz.

Además, en la teoría general de Einstein, el espacio y el tiempo dejan de considerarse entidades físicas separadas y se entienden como magnitudes interdependientes. El espaciotiempo se concibe como un entramado único que define la estructura misma del universo. En este marco, los sucesos ya no se localizan en puntos aislados del espacio ni en instantes discretos de tiempo, sino en coordenadas espaciotemporales que reflejan la interacción inseparable entre espacio y tiempo.
Medición de la longitud
Cuando se mide la longitud, tanto la precisión como la exactitud resultan esenciales.
Los instrumentos de medición de longitud abarcan desde simples reglas graduadas hasta sofisticados dispositivos como láseres o equipos GPS.
En los laboratorios, es posible alcanzar mediciones extremadamente precisas mediante el uso de interferómetros.
Operaciones con longitudes
En geometría euclidiana, las propiedades de las operaciones matemáticas también se aplican a las operaciones con longitudes.
La longitud de un segmento suele representarse con una letra minúscula (por ejemplo, a, b, c, ...).
Así, la congruencia de dos segmentos implica la igualdad de sus longitudes (a = b).
$$ a = b $$
Comparar dos segmentos no congruentes permite determinar cuál es más largo o más corto (a<b o a>b).
$$ a < b $$
La suma de dos segmentos corresponde a la longitud de un nuevo segmento que se obtiene uniendo sus extremos.
$$ a + b = c $$
La suma de longitudes cumple las siguientes propiedades:
- Conmutativa: $$ a+b = b+a $$
- Asociativa: $$ (a+b)+c = a+(b+c) $$
- Existencia del elemento neutro: $$ a+0 = 0+a = a $$
Y así sucesivamente.