Área

En geometría, el término área se refiere a la medida que indica la extensión de una superficie en el plano. También se puede definir como la cantidad de espacio contenida dentro del perímetro de una figura plana.

Es un concepto geométrico aplicado a figuras bidimensionales, es decir, aquellas que poseen dos dimensiones.

El área es una magnitud escalar que se expresa mediante un número real no negativo y que describe el tamaño de una región o figura situada en el plano.

La unidad estándar para medir el área es el metro cuadrado (m² o sqm), aunque también se emplean sus múltiplos y submúltiplos, como el centímetro cuadrado (cm²) o el kilómetro cuadrado (km²).

Según el ámbito, el área puede expresarse en otras unidades, como pulgadas cuadradas, o hectáreas (ha), muy utilizadas en agricultura y equivalentes a 10.000 metros cuadrados, entre otras.

Nota. El concepto de área ha sido objeto de estudio desde la Antigüedad. Matemáticos griegos como Euclides y Arquímedes desarrollaron las primeras teorías sistemáticas sobre el área, incluyendo métodos para calcular superficies de distintos polígonos y de la circunferencia. Es una noción esencial en numerosos campos más allá de las matemáticas puras, como la arquitectura, la ingeniería civil, la agricultura o la geografía, y resulta fundamental para la planificación y gestión de espacios.

Área en Física

En física, el área se considera una magnitud derivada que cuantifica la extensión de una superficie plana.

Se la denomina “derivada” porque se obtiene a partir de una magnitud fundamental: la longitud (L).

En el Sistema Internacional de Unidades (SI), la unidad estándar de área es el metro cuadrado (m²), que representa la superficie ocupada por un cuadrado cuyos lados miden exactamente 1 metro.

Desde el punto de vista del análisis dimensional, el área resulta del producto de dos longitudes, correspondientes a la base y la altura de una figura.

$$ \text{Área} = [L] \cdot [L] $$

Para calcular el área de figuras planas, como un rectángulo, se multiplica la longitud de la base por la altura.

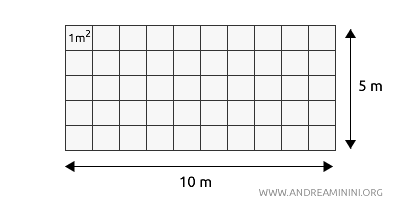
Por ejemplo, en un rectángulo cuya base mide 10 metros y cuya altura mide 5 metros:

$$ \text{Área} = \text{base} \times \text{altura} = (10 \, \text{m}) \times (5 \, \text{m}) = 50 \, \text{m}^2 $$

Este cálculo no solo proporciona el valor numérico ($10 \times 5 = 50$), sino que también recalca la importancia de multiplicar las unidades ($m \times m = m^2$).

En esencia, el área indica cuántos cuadrados de un metro de lado caben dentro de la superficie de dicho rectángulo.

Cálculo de Áreas

El método de cálculo del área varía según la figura geométrica de la que se trate:

• Área de un triángulo
  El área de un triángulo se calcula multiplicando la base por la altura y dividiendo entre dos. $$ A = \frac{Base \times Altura }{2} $$
• Área de un cuadrado
  El área de un cuadrado se obtiene elevando al cuadrado la longitud de uno de sus lados. $$ A = lado \times lado = lado ^2 $$
• Área de un rectángulo o paralelogramo
  El área de un rectángulo o de un paralelogramo se determina multiplicando la base por la altura. $$ A = Base \times Altura $$
• Área de un rombo
  El área de un rombo equivale al producto de sus diagonales d₁ y d₂, dividido entre dos. $$ A = \frac{d_1 \times d_2 }{2} $$
• Área de un trapecio
  El área de un trapecio se calcula multiplicando la altura por la suma de las bases mayor (Base) y menor (base), y dividiendo entre dos. $$ A = \frac{(Base + base) }{2} \times Altura $$
• Área de un círculo
  El área de un círculo se halla multiplicando el cuadrado de su radio por la constante pi ( π=3,14... ). $$ A = \pi r^2 $$
• Área de un polígono regular
  El área de un polígono regular se obtiene multiplicando el perímetro por el apotema y dividiendo entre dos. $$ A = \frac{Perímetro \times Apotema }{2} $$
• Área de una figura irregular
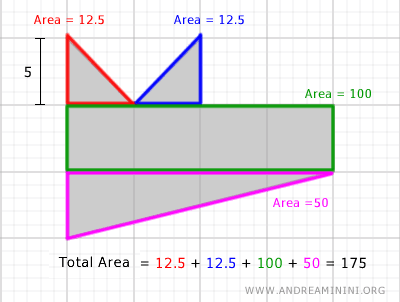
  Para calcular el área de una figura irregular, suele ser necesario descomponerla en figuras más simples o aplicar métodos de integración.
  

  

   

Múltiplos y submúltiplos del metro cuadrado

En el sistema métrico, la unidad estándar para medir áreas es el metro cuadrado (sqm o m²), que equivale a la superficie de un cuadrado cuyos lados miden un metro.

Entre sus múltiplos y submúltiplos figuran:

mm2	milímetros cuadrados
cm2	centímetros cuadrados
dm2	decímetros cuadrados
m2	metros cuadrados
dam2	decámetros cuadrados
hm2	hectómetros cuadrados
km2	kilómetros cuadrados

Cada unidad es cien veces mayor que la inmediata inferior y una centésima parte de la inmediata superior.

Por ejemplo, un metro cuadrado (m²) equivale a 100 decímetros cuadrados (dm²) y es la centésima parte de un decámetro cuadrado (dam²).

Conversión de unidades de área

El área puede expresarse en múltiplos o submúltiplos del metro cuadrado. Por ejemplo:

• Centímetro cuadrado ($cm^2$): equivalente a $10^{-4}$ metros cuadrados.
• Milímetro cuadrado ($mm^2$): equivalente a $10^{-6}$ metros cuadrados.
• Kilómetro cuadrado ($km^2$): equivalente a $10^6$ metros cuadrados.

Estos factores de conversión son fundamentales.

Por ejemplo, para convertir de $m^2$ a $cm^2$, se multiplica por $10^4$, ya que $1 \, cm = 10^{-2} \, m$. Así:

$$ 1 \, cm^2 = (10^{-2} \, m) \times (10^{-2} \, m) = 10^{-4} \, m^2 $$

El mismo principio se aplica a otras conversiones, como de milímetros cuadrados a metros cuadrados:

$$ 1 \, mm^2 = (10^{-3} \, m) \times (10^{-3} \, m) = 10^{-6} \, m^2 $$

Y para kilómetros cuadrados:

$$ 1 \, km^2 = (10^3 \, m) \times (10^3 \, m) = 10^6 \, m^2 $$

En general, al convertir unidades de área, es fundamental recordar que el factor de conversión se eleva al cuadrado.

Por ejemplo, si dispongo de un área de 100 m² y quiero convertirla a decímetros cuadrados (dm²), debo multiplicar por 10 al cuadrado, no simplemente por 10, como haría en el caso de una longitud. $$ 100 \ m^2 = 100 \cdot 10^2 \ dm^2 = 10000 \ dm^2 $$ Si deseo convertirla a centímetros cuadrados (cm²), aplico el cuadrado de 10². $$ 100 \ m^2 = 100 \cdot (10^2)^2 \ cm^2 = 100 \cdot 10^4 \ cm^2 = 10^6 \ cm^2 $$ Para convertirla a milímetros cuadrados (mm²), utilizo el cuadrado de 10³. $$ 100 \ m^2 = 100 \cdot (10^3)^2 \ mm^2 = 100 \cdot 10^6 \ mm^2 = 10^8 \ mm^2 $$ Y así sucesivamente.

Clases de equivalencia del área

Dos figuras geométricas pertenecen a la misma clase de equivalencia si poseen la misma área.

El área de las figuras geométricas define clases de equivalencia.

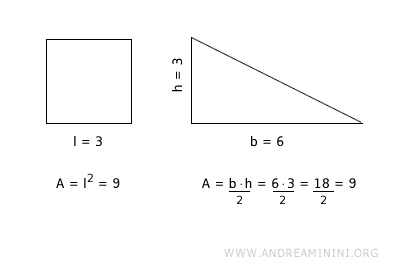
Los polígonos que tienen la misma área pertenecen a la misma clase de equivalencia y se denominan también polígonos equivalentes.

Y así sucesivamente.