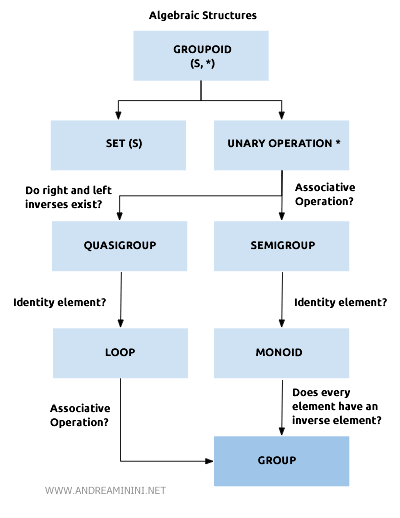
Grupos
¿Qué es un grupo?
- Un grupo es una estructura algebraica (G,*), que consta de:
- un conjunto no vacío (G ≠ Ø)
- una operación binaria $$ *: G × G \rightarrow G $$ que satisface tres propiedades fundamentales:
- Asociatividad: $$ (a*b)*c = a*(b*c) $$
- Elemento neutro: existe un elemento e en G tal que $$ a*e = e*a = a \ \ \forall \ a \in G $$
- Elemento inverso: cada elemento de G posee un inverso $$ a*(a)^{-1} = (a)^{-1}*a = e \ \ \forall \ a \in G $$
Desde la perspectiva del álgebra abstracta, un grupo es un monoide (S,*) en el que además cada elemento admite un inverso.
El número de elementos |G| que contiene el conjunto G determina el orden del grupo.
Los grupos se clasifican en función de la cantidad de elementos que los componen:
- Grupo finito: posee un número finito de elementos.
- Grupo infinito: contiene infinitos elementos.
Los grupos constituyen la base de la teoría de grupos y de la álgebra abstracta, un campo relativamente moderno dentro de las matemáticas.
Ejemplos prácticos
Ejemplo 1: El conjunto de los números enteros (Z) con la operación de suma (+)
- La suma es una operación binaria cerrada en Z, ya que la suma de dos números enteros produce otro número entero: $$ a+b = c \in Z \ \ \ \ \ \forall \ a,b \in Z $$
- Respeta la propiedad asociativa: para cualquier a, b, c ∈ Z, $$ (a + b) + c = a + (b + c) \ \ \ \ \ \forall \ a,b,c \in Z $$
- El elemento neutro es 0 ∈ Z, pues sumar cero a cualquier número entero no altera su valor: $$ a+0 = 0+a = a \ \ \ \ \ \forall \ a \in Z $$
- Todo número entero tiene un inverso aditivo en Z: la suma de un número con su opuesto da como resultado cero: $$ a+(-a) = (-a)+a = 0 \ \ \ \ \ \forall \ a \in Z $$
Por tanto, (Z, +) constituye un grupo aditivo.
Ejemplo 2: El conjunto de los números enteros (Z) con la operación de multiplicación (·) no forma un grupo, ya que no todos sus elementos tienen un inverso multiplicativo.
Por ejemplo, el inverso multiplicativo de 2 es 1/2, que no pertenece a Z: $$ 2 \cdot \frac{1}{2} = 1 $$
Nota: en este caso, el inverso multiplicativo sería 1/2. Aunque el conjunto Z con la operación de multiplicación cumple algunas propiedades propias de un grupo (cerradura, asociatividad, existencia de un elemento neutro), no todos los elementos poseen un inverso multiplicativo. Por ello, Z no constituye un grupo bajo la multiplicación. Para consultar el ejemplo completo.
Teoría de grupos
La teoría de grupos surgió en el siglo XIX, cuando los matemáticos se planteaban si era posible resolver todas las ecuaciones algebraicas mediante fórmulas generales.
Los trabajos pioneros de Ruffini, Abel y, sobre todo, de Évariste Galois demostraron que no siempre es así: la posibilidad de resolver una ecuación depende de las propiedades del grupo asociado a dicha ecuación. Este descubrimiento sentó las bases de la teoría de grupos.
Con el tiempo, el concepto evolucionó. En 1854, Arthur Cayley formuló por primera vez una definición abstracta de grupo, independiente de cualquier ecuación concreta.
Desde entonces, los grupos se han convertido en herramientas fundamentales para el análisis de estructuras y simetrías en prácticamente todas las áreas de las matemáticas, así como en numerosas aplicaciones científicas.
En el siglo XX, las contribuciones de Emmy Noether consolidaron la definición moderna de grupo y expandieron la teoría para abarcar tanto los grupos finitos como los infinitos.
Hoy en día, la teoría de grupos constituye uno de los pilares de las matemáticas modernas y de la álgebra abstracta.
Grupos abelianos
Un grupo se denomina abeliano cuando, además, satisface la propiedad conmutativa.
$$ (a*b)*c = a*(b*c) $$ $$ a*n = n*a = a $$ $$ a*a' = a'*a = n $$
Ejemplo
El conjunto de los números racionales Q forma un grupo abeliano con respecto a la operación de suma (Q,+).
Para cualesquiera tres números racionales (a, b, c), se verifica la propiedad asociativa:
$$ (a+b)+c = a+(b+c) $$
El elemento neutro es el cero:
$$ a+0 = 0+a = a $$
El inverso de un número es su opuesto:
$$ a + (-a) = (-a) + a = 0 $$
Asimismo, el cumplimiento de la propiedad conmutativa confirma que se trata de un grupo abeliano:
$$ a + b = b + a $$
Nota: Exceptuando el cero, el conjunto de los números racionales también constituye un grupo abeliano respecto a la multiplicación (Q,*), donde el número 1 actúa como elemento neutro y el recíproco 1/a como inverso multiplicativo.
Grupos no abelianos
Un grupo se considera no abeliano cuando no satisface la propiedad conmutativa.
Los grupos simétricos y los grupos diedrales son ejemplos representativos de grupos no abelianos.
Ejemplo
La multiplicación de matrices no es conmutativa.
Por tanto, el conjunto de matrices con la operación de multiplicación (M,*) constituye un grupo no abeliano.
$$ A \cdot B \ne B \cdot A $$
El producto se calcula aplicando la regla de multiplicación fila por columna.

Nota: En cambio, el conjunto de matrices (M,+) sí forma un grupo abeliano con respecto a la suma. El orden en que se suman las matrices en la suma de matrices no altera el resultado.
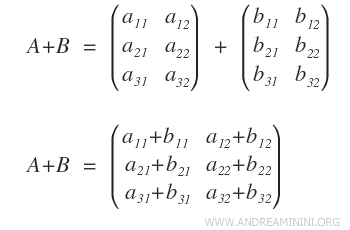
La tabla de multiplicación
Cuando un grupo está formado por un número finito de elementos, que no sea excesivamente grande, es posible representarlo mediante una tabla.
En cada fila y columna se coloca un elemento del grupo finito.
| a | b | ... | z | |
|---|---|---|---|---|
| a | a*a | a*b | ... | a*z |
| b | b*a | b*b | ... | b*z |
| ... | ||||
| z | z*a | z*b | ... | z*z |
Las celdas muestran el resultado de la operación binaria.
Ejemplo de grupo
Consideremos el grupo S compuesto por los elementos { 0,1,2,3,4,5,6,7 }, con la operación de suma módulo 8.
¿Qué es la suma módulo 8? Es una operación binaria propia de la aritmética modular o "aritmética del reloj". En la suma módulo 8, cualquier resultado mayor o igual que 8 se reemplaza por el resto que queda al dividir por 8. Por ejemplo: 5+2=7, 6+2=0, 7+2=1, etc.
La tabla de composición del grupo (S,+8) es la siguiente:
| a+b | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 0 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 0 | 1 |
| 3 | 3 | 4 | 5 | 6 | 7 | 0 | 1 | 2 |
| 4 | 4 | 5 | 6 | 7 | 0 | 1 | 2 | 3 |
| 5 | 5 | 6 | 7 | 0 | 1 | 2 | 3 | 4 |
| 6 | 6 | 7 | 0 | 1 | 2 | 3 | 4 | 5 |
| 7 | 7 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
Este conjunto constituye un grupo porque la operación binaria es asociativa:
$$ 1+(2+3) = (1+2)+3 = 6 $$
Existe un elemento neutro (0):
$$ 1+0=1 \\ 2+0=2 \\ \vdots $$
Y cada elemento posee un inverso aditivo:
$$ 1+7=0 \\ 2+6=0 \\ 3+5=0 \\ 4+4=0 \\ 5+3=0 \\ 6+2=0 \\ 7+1=0 $$
Orden de un grupo
El orden de un grupo finito es el número total de elementos que contiene el grupo. Se denota por $$ |G| $$ y constituye un dato esencial para comprender su estructura.
Ejemplo
Consideremos el grupo S { 0,1,2,3,4,5,6,7 }, con la operación de suma módulo 8. En este caso, el orden del grupo es 8, ya que consta de ocho elementos distintos:
$$ |S| = 8 $$
Es decir, el grupo S está formado por ocho elementos únicos.
Orden de un elemento en un grupo
El orden (o periodo) de un elemento g en un grupo (G, *), es el menor entero positivo h tal que, al aplicar la operación del grupo h veces sobre g, se obtiene el elemento neutro e:
$$ g^h = e $$
Si no existe tal entero h, se dice que el elemento g tiene orden infinito.
Si por el contrario, el orden de g es finito, el subgrupo generado por g, denotado <g>, está formado por:
$$ <g> = \{ e, g, g^1, g^2, ..., g^{h-1} \} $$
En tal caso, para cualquier par de enteros h y z (con h ≠ z), se verifica:
$$ g^h \equiv g^z \mod n $$
Ejemplo
En el grupo S { 0,1,2,3,4,5,6,7 }, con la operación de suma módulo 8, el orden de los elementos es el siguiente:
| Clase | Orden | Ejemplo |
|---|---|---|
| Clase 0 | 1 | 01 = 0 |
| Clase 1 | 8 | 18 = 0 |
| Clase 2 | 4 | 24 = 2 + 2 + 2 + 2 = 0 |
| Clase 3 | 8 | 38 = 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 = 0 |
| Clase 4 | 2 | 42 = 4 + 4 = 0 |
| Clase 5 | 8 | 58 = 5 + 5 + 5 + 5 + 5 + 5 + 5 + 5 = 0 |
| Clase 6 | 4 | 64 = 6 + 6 + 6 + 6 = 0 |
| Clase 7 | 8 | 78 = 7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 = 0 |
El orden de un elemento g es igual a la cardinalidad del subgrupo <g> generado por dicho elemento.
Ejemplo. La clase 2 tiene orden 4. El subgrupo <2> generado por el elemento 2 es:
$$ <2> = \{ 2, 4, 6, 0 \} $$
Este subgrupo contiene 4 elementos. Por tanto, la cardinalidad de <2> coincide con el orden del elemento 2, que es 4.
Potenciación en los grupos
En teoría de grupos, el concepto de potenciación está directamente ligado a la operación del grupo, y no debe confundirse con la potenciación habitual en la aritmética de números reales.
Elevar un elemento g a la n-ésima potencia equivale a aplicar n veces la operación del grupo sobre el propio g:
$$ g^n = g \ast g \ast \dots \ast g \quad (n \text{ veces}) $$
Ejemplo
Por ejemplo, g4 significa:
$$ g^4 = g \ast g \ast g \ast g $$
Nota: El resultado depende de la operación del grupo. Si la operación es la suma (+), entonces g4 = g + g + g + g. Si es la multiplicación (*), g4 = g \ast g \ast g \ast g.
Para exponentes negativos, por ejemplo g-4, se tiene:
$$ g^{-4} = g^{-1} \ast g^{-1} \ast g^{-1} \ast g^{-1} $$
Por definición, para exponente cero siempre se obtiene el elemento neutro del grupo:
$$ g^0 = e $$
Nota: En grupos aditivos (G,+), g0 = 0; en grupos multiplicativos (G,*), g0 = 1.
Grupos cíclicos
Un grupo se dice cíclico si existe un elemento g que genera todo el grupo, es decir, si todos los elementos de G se pueden obtener aplicando repetidamente la operación del grupo sobre g.
En otras palabras, el subgrupo generado por g coincide con el conjunto completo G.
Por ejemplo, en la aritmética modular de base 8 con la operación de suma:
$$ G = (\{0,1,2,3,4,5,6,7\},+) $$
Este grupo es cíclico porque el elemento 1 actúa como generador y permite obtener todos los elementos de G mediante sumas sucesivas:
$$ <1> = \{1, 2, 3, 4, 5, 6, 7, 0\} = G $$
Por tanto, G es un grupo cíclico de orden 8.
Propiedades de los grupos cíclicos
Los grupos cíclicos son siempre abelianos, y todos sus subgrupos son también cíclicos.
Además, el orden de cualquier subgrupo divide al orden del grupo, y para cada divisor de dicho orden existe un único subgrupo correspondiente.
Subgrupos cíclicos infinitos
Un subgrupo cíclico es infinito si su generador tiene orden infinito, es decir, si sus potencias producen elementos distintos para todo exponente entero.