Grupos simétricos
Un grupo simétrico \( (S_n, *) \) sobre un conjunto \( S \) está formado por el conjunto \( S_n \) de todas las permutaciones de los elementos de \( S \), junto con la operación binaria de composición de funciones: \( f * g = f \circ g = f[g] \).
En este contexto, cada permutación se interpreta como una función biyectiva, o correspondencia \( \sigma \), del conjunto \( S \) en sí mismo:
$$ \sigma : S \rightarrow S $$
El conjunto \( S_n \) está constituido por todas las correspondencias biyectivas de \( S \) sobre sí mismo:
$$ S_n = \{ \sigma_1, \sigma_2, \dots, \sigma_k \} $$
El grupo simétrico \( (S_n, *) \) es un grupo de orden \( n! \), ya que existen \( n! \) permutaciones posibles de \( n \) elementos de un conjunto finito \( S \).
Nota: Los grupos simétricos de conjuntos finitos con el mismo número de elementos \( n \) son isomorfos. Además, para \( n > 2 \), estos grupos son no abelianos, es decir, no conmutativos.
Ejemplo práctico
Consideremos un conjunto con tres elementos \( (n = 3) \):
$$ S = \{ 1, 2, 3 \} $$
Existen \( n! = 3 \cdot 2 \cdot 1 = 6 \) permutaciones posibles de estos elementos:
$$ S_n = \begin{Bmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \\ 2 & 1 & 3 \\ 2 & 3 & 1 \\ 3 & 1 & 2 \\ 3 & 2 & 1 \end{Bmatrix} $$
Si partimos de \( S = \{ 1, 2, 3 \} \), una permutación posible \( \sigma \) es:
$$ \sigma : (1, 2, 3) \rightarrow (2, 3, 1) $$
Esta correspondencia biyectiva \( \sigma \) se representa en notación tabular como:
$$ \sigma = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} $$
En cada columna, se indica cómo se mapea cada elemento de \( S \) sobre sí mismo.
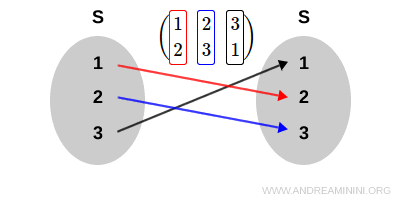
Nota: La permutación \( \sigma \) actúa de la siguiente forma: $$ \sigma(1) = 2 \\ \sigma(2) = 3 \\ \sigma(3) = 1 $$ Por ejemplo, \( \sigma(1) = 2 \), ya que \( 1 \rightarrow 2 \); \( \sigma(3) = 1 \), ya que \( 3 \rightarrow 1 \).
El conjunto de todas estas permutaciones \( \sigma \) forma el grupo simétrico \( (S_n, *) \), con la operación de composición:
$$ (S_n, *) $$
Nota: Este grupo tiene orden \( n! = 6 \), ya que \( S_n \) contiene 6 elementos: $$ S_n = \begin{Bmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \\ 2 & 1 & 3 \\ 2 & 3 & 1 \\ 3 & 1 & 2 \\ 3 & 2 & 1 \end{Bmatrix} $$
La operación de composición * es una operación binaria entre dos permutaciones, es decir, entre dos elementos de \( S_n \).
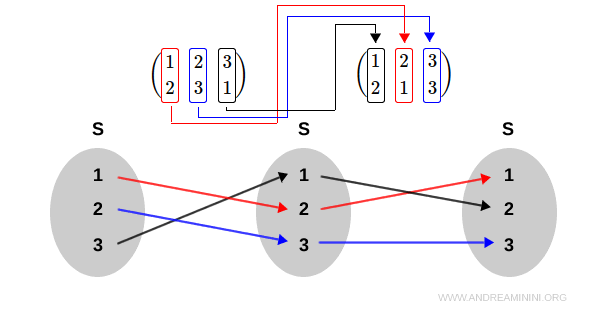
Por ejemplo, consideremos las siguientes permutaciones:
$$ \sigma_1 : (1, 2, 3) \rightarrow (2, 1, 3) = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} $$
$$ \sigma_2 : (1, 2, 3) \rightarrow (2, 3, 1) = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} $$
La composición de estas permutaciones se expresa como:
$$ \sigma_1 * \sigma_2 = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} * \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix} $$
La composición se realiza de derecha a izquierda: \( f * g = f[g] \), es decir, primero se aplica \( \sigma_2 \), luego \( \sigma_1 \).
El resultado es la permutación:
$$ \sigma_1 * \sigma_2 = \begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix} $$
Una representación gráfica facilita la comprensión de este proceso:
Explicación: - \( \sigma_2(1) = 2 \), \( \sigma_1(2) = 1 \), por lo que \( \sigma_1 * \sigma_2(1) = 1 \). 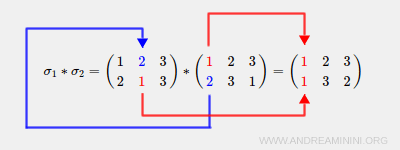
- \( \sigma_2(2) = 3 \), \( \sigma_1(3) = 3 \), por lo que \( \sigma_1 * \sigma_2(2) = 3 \). 
- \( \sigma_2(3) = 1 \), \( \sigma_1(1) = 2 \), por lo que \( \sigma_1 * \sigma_2(3) = 2 \). 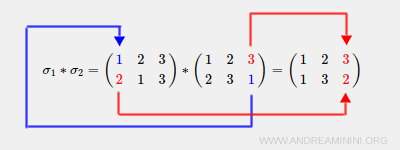
¿Es un grupo abeliano o no abeliano?
El grupo simétrico \( (S_n, *) \), que describe las permutaciones de los elementos de \( S \), es un grupo de orden \( n! \). Cuando \( n > 2 \), el grupo es claramente no abeliano, ya que no cumple la propiedad conmutativa.
Comprobación: En la composición anterior hemos obtenido: $$ \sigma_1 * \sigma_2 = \begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix} $$ Si invertimos el orden: $$ \sigma_2 * \sigma_1 = \begin{pmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{pmatrix} $$ Por tanto: $$ \sigma_1 * \sigma_2 \ne \sigma_2 * \sigma_1 $$ El grupo \( (S_n, *) \) no es conmutativo: es un grupo no abeliano.
Y así sucesivamente.