Estructuras Algebraicas
Definición de una Estructura Algebraica
Una estructura algebraica está compuesta por un conjunto S y una o varias operaciones definidas sobre S. $$ (S,*) $$
Si incluye solo una operación, se denomina grupoide.
Si la operación en un grupoide es asociativa, se le llama semigrupo.
Cuando un semigrupo contiene un elemento identidad, lo conocemos como un monoide.
¿Qué es una Operación?
Una operación es una función que asocia elementos del conjunto S con otros elementos del mismo conjunto.
$$ *: S \rightarrow S $$
Se trata de una operación binaria cuando implica combinar dos elementos de S para obtener otro elemento de S.
$$ *: S×S \rightarrow S $$
Un Ejemplo de Estructura Algebraica
Ejemplo 1
Tomemos el conjunto de números enteros Z con la suma (+) como operación.
$$ ( Z , + ) $$
Esta configuración forma una estructura algebraica donde cada par de enteros (sumandos) genera otro entero (la suma).
$$ +: ZxZ \rightarrow Z $$
Nota: Si el resultado de la operación no estuviera dentro del conjunto Z, entonces no sería una estructura algebraica.
Ejemplo 2
Consideremos el conjunto de números del 1 al 10 con la multiplicación (*) como operación.
$$ S = ( 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ) $$
Aquí, (S,*) no forma una estructura algebraica porque algunos productos quedan fuera del conjunto S.
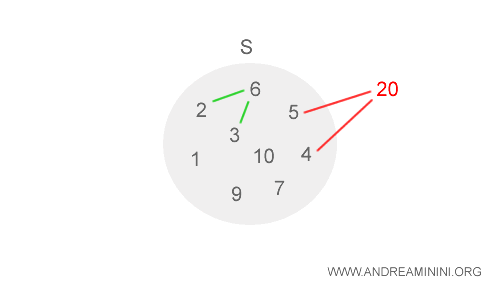
Por ejemplo, multiplicar 4 y 5 da 20, que no es un elemento de S.
$$ (1*2)=2 \\ (2*3)=6 \\ (4*5)=20 $$
Esto no cumple con las condiciones necesarias para ser una estructura algebraica.
Un mismo conjunto S puede ser una estructura algebraica bajo una operación pero no bajo otra. Por ejemplo, el conjunto de números naturales N forma una estructura algebraica (N,+) con la suma, pero no con la resta (N,-), ya que restar dos números naturales podría dar como resultado un número negativo, que no pertenece al conjunto.
La Tabla de Verdad
Cuando una estructura algebraica tiene un número finito de elementos, es posible representarla mediante una tabla de verdad.
Ejemplo
Tenemos un conjunto S compuesto por tres elementos {a,b,c} y una operación |
$$ (S,|) $$
La operación asocia cada par de elementos en SxS con otro elemento dentro de S.
A continuación, la tabla de verdad:
| a | b | c | |
|---|---|---|---|
| a | a | a | b |
| b | c | b | a |
| c | a | b | c |
Esto representa una estructura algebraica simple, específicamente un grupoide, con una sola operación.
Y así sucesivamente.
Nota Importante. La lógica usada para asociar pares de elementos con resultados no está predeterminada. Por ejemplo, el resultado de (a,b) podría ser c, a o b, dependiendo de la función o del circuito lógico elegido. El criterio esencial para una estructura algebraica es que el resultado también pertenezca al conjunto S.