Campo matemático

Un campo es un conjunto no vacío K, dotado de dos operaciones binarias internas (suma y multiplicación), representadas por + y · $$ (\ K \ , \ + \ , \ \cdot \ ) $$, que cumplen las siguientes propiedades:

1. Propiedad conmutativa $$ x+y=y+x $$ $$ x·y=y·x $$
2. Propiedad asociativa $$ (x+y)+z = x+(y+z) $$ $$ (x·y)·z = x·(y·z) $$
3. Propiedad distributiva de la multiplicación sobre la suma $$ (x+y)·z = (x·z)+(y·z) $$ $$ x·(y+z) = (x·y)+(x·z) $$
4. Elemento neutro aditivo
   Existe al menos un elemento neutro aditivo tal que, para todo elemento x de K, $$ 0+x = x+0 = x \ \ \ \ \forall x \in K $$
5. Elemento neutro multiplicativo
   Existe al menos un elemento neutro multiplicativo tal que, para todo elemento x de K, $$ 1·x = x·1 = x \ \ \ \ \forall x \in K $$
6. Inverso aditivo (elemento opuesto)
   Para cada elemento x de K, existe un elemento opuesto -x tal que su suma con x es el neutro aditivo: $$ x+(-x) = 0 \ \ \ \ \forall x \in K $$
7. Inverso multiplicativo
   Para todo elemento distinto de cero \(x \neq 0\) en K, existe un inverso multiplicativo \(x^{-1}\) tal que su producto con x es el neutro multiplicativo: $$ x \cdot x^{-1} = x^{-1} \cdot x = 1 \ \ \ \ \forall x \in K $$

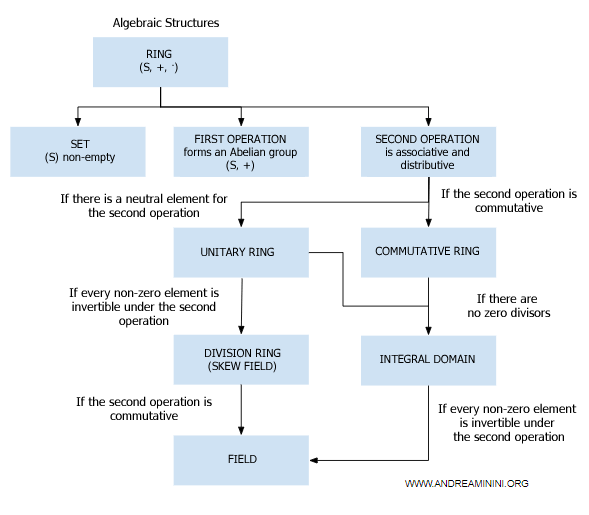
Nota. En términos sencillos, un campo es un anillo (S,+,*) en el que la segunda operación, * (multiplicación), también es conmutativa, existe un elemento neutro multiplicativo y todo elemento distinto de cero posee un inverso multiplicativo.

Un campo cuyos elementos son números se denomina campo numérico (o campo de números).

El campo numérico es un caso particular de campo general, que puede definirse sobre cualquier tipo de elementos (por ejemplo, números, polinomios, funciones u otras entidades algebraicas).

Un ejemplo práctico

Consideremos el conjunto de los números racionales Q con las operaciones de suma (+) y multiplicación (·).

$$ (Q, + , \cdot ) $$

Para determinar si esta estructura algebraica es un campo, debemos comprobar que ambas operaciones cumplen las propiedades requeridas.

Primera operación (+)

Verifiquemos si la primera operación define un grupo abeliano (Q,+).

• La suma es una operación interna en Q: $$ \forall \ a,b \in Q \ \ \ \ a+b \in Q $$
• La suma es asociativa: $$ \forall \ a,b,c \in Q \ \ \ (a+b)+c = a+(b+c) $$
• Existe un neutro aditivo: $$ \forall \ a \in Q \ \ \ a + 0 = 0+a = a $$
• Todo elemento de Q posee un inverso aditivo: $$ \forall \ a \in Q \ \ \ a + (-a) = (-a)+a = 0 $$

Por lo tanto, la suma define un grupo (Q,+) sobre el conjunto de los números racionales.

Además, como la suma es conmutativa en Q, el grupo (Q,+) es abeliano:

$$ \forall \ a,b \in Q \ \ \ a+b = b+a $$

La primera operación (+) satisface así todas las condiciones requeridas para un campo.

Segunda operación (·)

Ahora comprobemos si la multiplicación en Q cumple con las propiedades necesarias.

• La multiplicación es una operación interna en Q: $$ \forall \ a,b \in Q\ \ \ \ a \cdot b \in Q $$
• Es distributiva respecto a la suma, por ambos lados: $$ \forall \ a,b,c \in Q \ \ \ \ a \cdot (b+c) = ab+ac $$ $$ \forall \ a,b,c \in Q \ \ \ \ (a+b) \cdot c = ac+bc $$
• Es asociativa: $$ \forall \ a,b,c \in Q \ \ \ (a \cdot b) \cdot c = a \cdot (b \cdot c) $$
• Existe un neutro multiplicativo: $$ \forall \ a \in Q \ \ \ a \cdot 1 = 1 \cdot a = a $$
• Todo elemento no nulo de Q posee un inverso multiplicativo: $$ \forall \ a \in Q \ , \ a \ne 0 \ \ \ a \cdot a^{-1} = a^{-1} \cdot a = 1 $$

Además, la multiplicación es conmutativa:

$$ \forall \ a,b \in Q\ \ \ \ a \cdot b = b \cdot a $$

Por tanto, la segunda operación (·) también satisface todas las condiciones para definir un campo.

Concluimos entonces que el anillo (Q,+,·) es un campo.

Campos conmutativos

Un campo se denomina conmutativo si el orden en que se efectúan la suma o la multiplicación no altera el resultado.

En general, la mayoría de los campos que se estudian son conmutativos.

Ejemplo

El campo de los números reales es conmutativo, ya que tanto la suma como la multiplicación son independientes del orden:

$$ (3 + 4) = (4 + 3) = 7 $$

$$ (2 \cdot 5) = (5 \cdot 2) = 10 $$

Notas adicionales

Algunos aspectos complementarios sobre los campos:

• Un campo también se conoce como anillo de división conmutativo
  Un campo también se denomina “anillo de división conmutativo” porque es un anillo de división en el cual la multiplicación es conmutativa. Es decir, todo elemento no nulo tiene un inverso multiplicativo, y la multiplicación entre dos elementos cualesquiera cumple: \(a \cdot b = b \cdot a\). Esta propiedad lo distingue de un anillo de división general, donde la multiplicación puede no ser conmutativa. Así pues, un campo es un caso particular dentro de los anillos de división.
• Diferencia entre un campo general y un campo numérico
  La diferencia entre un “campo general” y un “campo numérico” es sutil pero relevante en el contexto matemático. Un campo numérico es un caso particular de campo general, en el que todos sus elementos son números. Por tanto, aunque todo campo numérico es un campo, no todo campo es necesariamente un campo numérico.

Y así sucesivamente.