Anillos en álgebra abstracta

En esta definición se ha utilizado el conjunto de los números reales R por motivos de simplicidad, aunque en realidad el conjunto puede ser cualquiera.

Las dos operaciones (+) y (·) deben satisfacer condiciones distintas.

En particular, la primera operación en un anillo debe constituir un grupo abeliano (R,+)

Nota: En un anillo, la suma debe ser conmutativa, mientras que el producto no está obligado a serlo. Además, un anillo debe poseer un elemento neutro e inversos aditivos respecto a la suma, pero no se requiere que la multiplicación tenga ni elemento neutro ni inversos. También es fundamental el orden de las operaciones: la estructura (R,+,·) es un anillo, pero (R,·,+) no lo es, ya que el cero carece de inverso. En otras palabras, (R,+) sí forma un grupo abeliano, mientras que (R,·) ni siquiera constituye un grupo.

Por convención, se suele denominar "suma" a la primera operación y "producto" a la segunda.

Sin embargo, estas operaciones no tienen por qué corresponder literalmente a una suma o un producto: podrían representar cualquier otra operación.

Un ejemplo práctico

El conjunto de matrices cuadradas M_n(Z) de orden n (es decir, con n filas y n columnas) forma un anillo sobre el conjunto de los números enteros Z, con suma definida elemento a elemento y producto fila por columna:

$$ (M_n(Z),+, \cdot) $$

Ambas operaciones son cerradas, es decir, el resultado es siempre una matriz cuadrada.

$$ M_n(Z) \ × \ M_n(Z) \rightarrow M_n(Z) $$

Veamos ahora si se cumplen las demás propiedades necesarias.

Primera operación

La suma elemento a elemento de dos matrices cuadradas es conmutativa:

$$ A + B = B + A \ \ \ \forall \ A, B \in M_n(Z) $$

También es asociativa:

$$ (A + B) + C = A + (B + C) \ \ \ \forall \ A, B, C \in M_n(Z) $$

El elemento neutro aditivo es la matriz nula.

Y para cada matriz cuadrada existe un inverso aditivo:

$$ A + (-A) = 0 \ \ \ \forall \ A \in M_n(Z) $$

Por lo tanto, se cumplen todas las propiedades requeridas para la primera operación en un anillo.

Nota: La estructura (M_n(Z),+) constituye un grupo, ya que el conjunto es no vacío, la operación es cerrada, se cumple la asociatividad y existen tanto el elemento neutro como los inversos. Como además la operación es conmutativa, (M_n(Z),+) forma un grupo abeliano.

Segunda operación

La segunda operación es el producto de matrices fila por columna.

Este producto es asociativo:

$$ (A \cdot B) \cdot C = A \cdot (B \cdot C) \ \ \ \forall \ A, B, C \in M_n(Z) $$

Y también es distributivo:

$$ (A + B) \cdot C = A \cdot C + B \cdot C \ \ \ \forall \ A, B, C \in M_n(Z) $$

$$ A \cdot ( B + C ) = A \cdot B + A \cdot C \ \ \ \forall \ A, B, C \in M_n(Z) $$

Por tanto, la segunda operación cumple igualmente con las propiedades exigidas en un anillo.

Conclusión

En conclusión, ambas operaciones verifican todos los requisitos que definen un anillo.

Por lo tanto, la estructura algebraica (M_n(Z),+,*) es un anillo.

Tipos de anillos

Existen anillos que además cumplen otras propiedades adicionales que no son obligatorias:

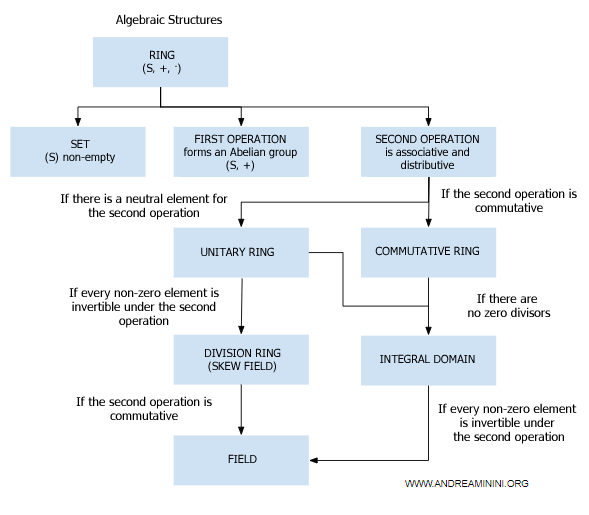
Entre ellas se encuentran:

• Anillo conmutativo
  Un anillo (R,+,·) es conmutativo si el producto también es conmutativo: $$ a \cdot b = b \cdot a \ \ \forall \ a,b \in R $$
• Anillo unitario
  Un anillo (R,+,·) es unitario si existe un elemento neutro para el producto: $$ a \cdot 1 = 1 \cdot a = a \ \ \forall \ a \in R $$
• Dominio de integridad
  Un anillo es un dominio de integridad si es conmutativo, unitario y no tiene divisores de cero: $$ \forall \ a,b \in R \ \ ab = 0 \ \Rightarrow \ a = 0 \ \text{ó} \ b = 0 $$
• Anillo de división
  Un anillo de división (R,+,·) es unitario y cada elemento no nulo admite un inverso multiplicativo: $$ a \cdot a^{-1} = 1 \ \ \forall \ a \neq 0 \in R $$
• Cuerpo
  Un cuerpo (R,+,·) es un anillo conmutativo y unitario en el cual todo elemento no nulo posee un inverso multiplicativo: $$ a \cdot a^{-1} = 1 \ \ \forall \ a \neq 0 \in R $$