Ejercicios resueltos sobre anillos
Algunos ejercicios prácticos resueltos para consolidar el estudio de los anillos.
Ejercicio 1
Queremos determinar si el conjunto de los enteros módulo 5 $$ \mathbb{Z}_5 = \{ 0, 1, 2, 3, 4 \} $$ provisto de la suma y el producto módulo 5, constituye un anillo:
$$ (\mathbb{Z}_5 , +_5, \cdot_5) $$
Como $\mathbb{Z}_5$ es un conjunto finito, podemos construir explícitamente su tabla de suma:
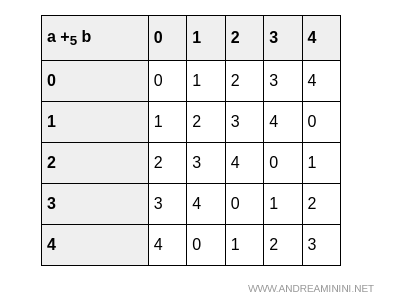
Y del mismo modo, su tabla de multiplicación:
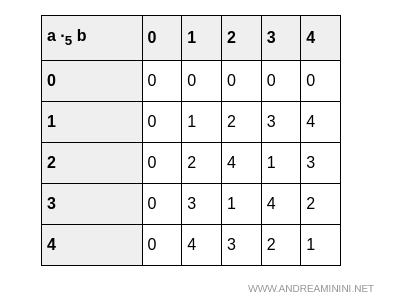
Ambas operaciones son cerradas en $\mathbb{Z}_5$, cumpliendo así la primera condición para que sea un anillo.
Procedamos ahora a verificar los demás axiomas.
Primera operación: suma ($+_5$)
La suma módulo 5 en $\mathbb{Z}_5$ es conmutativa:
$$ a +_5 b = b +_5 a \quad \forall \ a, b \in \mathbb{Z}_5 $$
También es asociativa:
$$ (a +_5 b) +_5 c = a +_5 (b +_5 c) \quad \forall \ a, b, c \in \mathbb{Z}_5 $$
El neutro aditivo es $0$:
$$ a +_5 0 = 0 +_5 a = a \quad \forall \ a \in \mathbb{Z}_5 $$
Todo elemento de $\mathbb{Z}_5$ posee inverso aditivo. Por ejemplo:
$0 + 0 = 0$, $1 + 4 = 0$, $2 + 3 = 0$, etc.
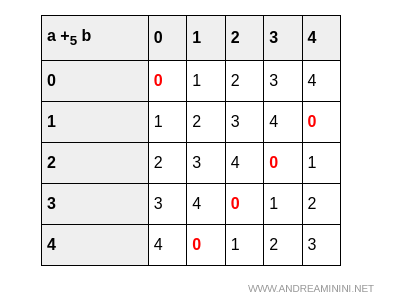
Por tanto, se cumplen todos los axiomas de la estructura aditiva de un anillo.
Nota: La estructura $(\mathbb{Z}_5, +)$ es un grupo, pues $\mathbb{Z}_5$ es no vacío, la suma módulo 5 es cerrada, asociativa, posee elemento neutro ($0$) y cada elemento tiene su inverso. Además, como la operación es conmutativa, $(\mathbb{Z}_5, +)$ es un grupo abeliano, cumpliendo así el primer requisito fundamental para ser un anillo.
Segunda operación: multiplicación ($\cdot_5$)
La multiplicación módulo 5 en $\mathbb{Z}_5$ es asociativa:
$$ (a \cdot_5 b) \cdot_5 c = a \cdot_5 (b \cdot_5 c) \quad \forall \ a, b, c \in \mathbb{Z}_5 $$
Además, la multiplicación distribuye sobre la suma, tanto por la izquierda como por la derecha:
$$ (a +_5 b) \cdot_5 c = a \cdot_5 c +_5 b \cdot_5 c \quad \forall \ a, b, c \in \mathbb{Z}_5 $$
$$ a \cdot_5 (b +_5 c) = a \cdot_5 b +_5 a \cdot_5 c \quad \forall \ a, b, c \in \mathbb{Z}_5 $$
Por tanto, se cumplen también los axiomas correspondientes a la multiplicación.
Conclusión
Como ambas operaciones satisfacen los axiomas requeridos, podemos concluir que:
La estructura algebraica $(\mathbb{Z}_5, +, \cdot)$ es un anillo.
Ejercicio 2
Queremos determinar si la función $$ f(x) = |x| $$ define un homomorfismo de anillos entre $$ (\mathbb{Z}, +, \cdot) \quad \text{y} \quad (\mathbb{Z}', +, \cdot), $$ donde $\mathbb{Z} = \mathbb{Z}'$.
Comenzamos verificando si $f$ preserva el producto, como exige la definición de homomorfismo de anillos:
$$ f(a \cdot b) = f(a) \cdot f(b) $$
$$ |a \cdot b| = |a| \cdot |b| $$
Esta igualdad se verifica siempre, ya que el valor absoluto de un producto es igual al producto de los valores absolutos.
Nota: El valor absoluto del producto es siempre no negativo, al igual que el producto de dos valores absolutos. Por tanto, ambos lados coinciden.
Examinemos ahora si $f$ preserva la suma:
$$ f(a + b) = f(a) + f(b) $$
$$ |a + b| = |a| + |b| $$
Esta igualdad no se verifica en general - en particular, falla cuando $a$ y $b$ tienen signos opuestos.
Por ejemplo, si $a = 2$ y $b = -3$:
$$ |2 + (-3)| \ne |2| + |-3| $$
$$ |-1| \ne 2 + 3 $$
$$ 1 \ne 5 $$
Dado que la función no preserva la suma, no cumple las propiedades que definen un homomorfismo de anillos.
Concluimos, por tanto, que la función $$ f(x) = |x| $$ no es un homomorfismo de anillos entre $(\mathbb{Z}, +, \cdot)$ y $(\mathbb{Z}', +, \cdot)$.
Ejercicio 3
¿El conjunto de los enteros módulo 6 $$ \mathbb{Z}_6 = \{ 0, 1, 2, 3, 4, 5 \} $$ provisto de la suma y el producto módulo 6, constituye un anillo?
$$ (\mathbb{Z}_6 , +_6, \cdot_6) $$
Como $\mathbb{Z}_6$ es un conjunto finito, comenzamos construyendo su tabla de suma:
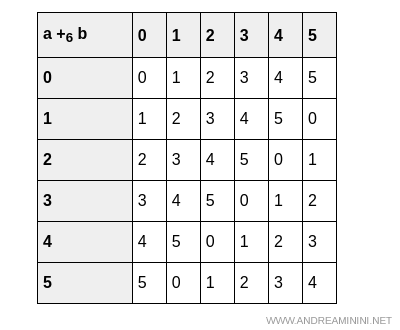
Y a continuación su tabla de multiplicación:
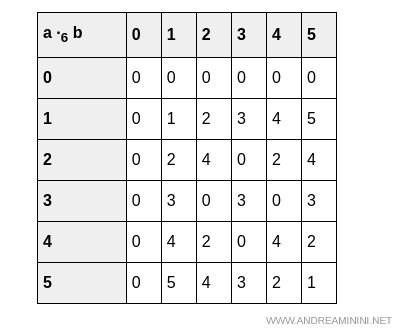
Ambas operaciones son cerradas en $\mathbb{Z}_6$, por lo que se cumple la primera condición para que sea un anillo.
Vamos ahora a comprobar si se satisfacen los demás axiomas.
Primera operación: suma ($+_6$)
La suma módulo 6 es conmutativa en $\mathbb{Z}_6$:
$$ a +_6 b = b +_6 a \quad \forall \ a, b \in \mathbb{Z}_6 $$
También es asociativa:
$$ (a +_6 b) +_6 c = a +_6 (b +_6 c) \quad \forall \ a, b, c \in \mathbb{Z}_6 $$
El neutro aditivo es $0$:
$$ a +_6 0 = 0 +_6 a = a \quad \forall \ a \in \mathbb{Z}_6 $$
Además, cada elemento de $\mathbb{Z}_6$ posee un inverso aditivo. Por ejemplo: $0 + 0 = 0$, $1 + 5 = 0$, $2 + 4 = 0$, $3 + 3 = 0$, etc.
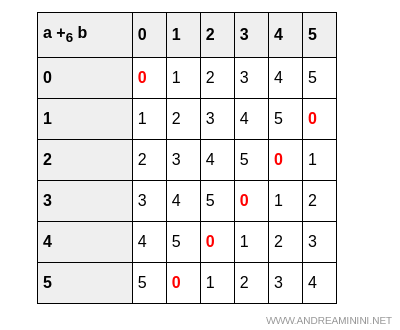
Por tanto, la operación de suma cumple todos los axiomas requeridos en un anillo.
Nota: La estructura $(\mathbb{Z}_6, +)$ es un grupo, ya que $\mathbb{Z}_6$ es no vacío, la suma módulo 6 es cerrada y asociativa, existe un neutro ($0$), y cada elemento tiene su inverso. Además, como la operación es conmutativa, $(\mathbb{Z}_6, +)$ es un grupo abeliano.
Segunda operación: multiplicación ($\cdot_6$)
La multiplicación módulo 6 es asociativa en $\mathbb{Z}_6$:
$$ (a \cdot_6 b) \cdot_6 c = a \cdot_6 (b \cdot_6 c) \quad \forall \ a, b, c \in \mathbb{Z}_6 $$
Además, satisface las leyes distributivas con respecto a la suma:
$$ (a +_6 b) \cdot_6 c = a \cdot_6 c +_6 b \cdot_6 c \quad \forall \ a, b, c \in \mathbb{Z}_6 $$
$$ a \cdot_6 (b +_6 c) = a \cdot_6 b +_6 a \cdot_6 c \quad \forall \ a, b, c \in \mathbb{Z}_6 $$
Por tanto, también la multiplicación satisface los axiomas necesarios.
Conclusión
Ambas operaciones cumplen los axiomas que definen un anillo.
Por tanto, podemos afirmar que la estructura algebraica $(\mathbb{Z}_6, +, \cdot)$ es un anillo.
Ejercicio 4
Queremos determinar si la función $$ f(x) = 3x $$ define un homomorfismo de anillos entre $$ (\mathbb{Z}_6, +, \cdot) \quad \text{y} \quad (\mathbb{Z}_6', +, \cdot), $$ donde tanto la suma como la multiplicación se consideran módulo 6.
Como primer paso, construimos la tabla de suma módulo 6:

Y a continuación, la tabla de multiplicación:

Comprobemos ahora si la función cumple la primera condición para ser un homomorfismo de anillos:
$$ f(a + b) = f(a) + f(b) $$
Dado que $f(x) = 3x$, tenemos:
$$ 3 \cdot (a + b) = 3a + 3b $$
Esta igualdad se verifica módulo 6, por lo que la función preserva la suma.
Comprobemos ahora si $f(x)$ también preserva la multiplicación:
$$ f(a \cdot b) = f(a) \cdot f(b) $$
Sustituyendo:
$$ 3 \cdot (a \cdot b) = (3a) \cdot (3b) $$
Utilizando la asociatividad y las propiedades de la aritmética modular, se verifica que la igualdad es válida.
Por tanto, la función $f(x) = 3x$ es un homomorfismo de anillos de $(\mathbb{Z}_6, +, \cdot)$ en sí mismo.
Verificación
Como estamos trabajando con un anillo finito y pequeño, resulta útil mostrar explícitamente las tablas asociadas a la función, para confirmar el resultado.
En el caso de la suma, tanto $3(a + b)$ como $3a + 3b$ producen la misma tabla:
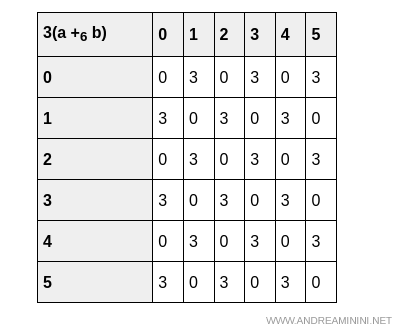
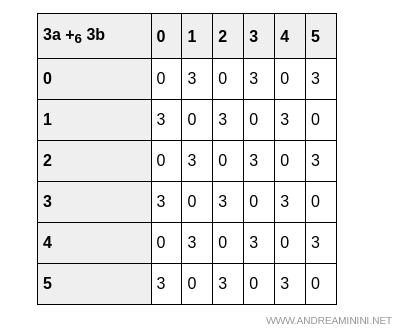
Del mismo modo, en la multiplicación, las tablas $3(a \cdot b)$ y $(3a) \cdot (3b)$ producen el mismo resultado:
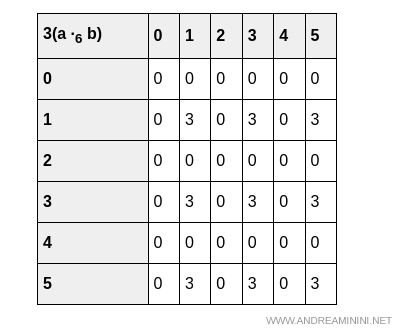
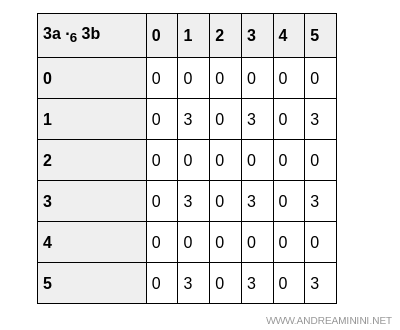
Esta verificación exhaustiva confirma plenamente el resultado:
La aplicación $f(x) = 3x$ define un homomorfismo de anillos entre $(\mathbb{Z}_6, +, \cdot)$ y $(\mathbb{Z}_6, +, \cdot)$.