Isomorfismo entre anillos

Un isomorfismo entre dos anillos A y A' es una aplicación biyectiva $$ \phi: A \rightarrow A' $$ que satisface las siguientes propiedades para todo par de elementos $a, b \in A$: $$ \phi(a + b) = \phi(a) + \phi(b) $$ $$ \phi(a \cdot b) = \phi(a) \cdot \phi(b) $$ donde $a$ y $b$ son elementos de A, y $\phi(a + b)$ y $\phi(a \cdot b)$ son elementos de A'.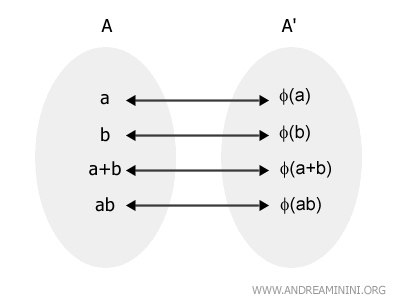

Cuando existe tal aplicación, se dice que los dos anillos son isomorfos:

$$ A \simeq A' $$

Esta relación es una relación de equivalencia: ambas estructuras algebraicas comparten las mismas propiedades internas.

En este contexto, se dice que las dos estructuras algebraicas pertenecen a la misma clase de isomorfismo.

Un ejemplo concreto

Consideremos el conjunto de los números complejos $\mathbb{C}$ y la aplicación que asigna a cada número complejo $$ z = a + bi $$ su conjugado complejo $z'$:

$$ z' = \operatorname{Re}(z) - \operatorname{Im}(z) \cdot i $$

Esta aplicación asocia a cada número complejo $z \in \mathbb{C}$ otro elemento de $\mathbb{C}$, y la correspondencia es biyectiva.

Por tanto, esta aplicación define un isomorfismo de $\mathbb{C}$ sobre sí mismo.

Por ejemplo, consideremos los números complejos:

$$ z_1 = 3 + 4i $$

$$ z_2 = 5 - 2i $$

Sus conjugados, mediante esta aplicación, son:

$$ z'_1 = \operatorname{Re}(z_1) - \operatorname{Im}(z_1) \cdot i = 3 - 4i $$

$$ z'_2 = \operatorname{Re}(z_2) - \operatorname{Im}(z_2) \cdot i = 5 + 2i $$

Recíprocamente, a partir de los conjugados $z'_1 = 3 - 4i$ y $z'_2 = 5 + 2i$, se pueden recuperar los números originales:

$$ z_1 = \operatorname{Re}(z'_1) - \operatorname{Im}(z'_1) \cdot i = 3 + 4i $$

$$ z_2 = \operatorname{Re}(z'_2) - \operatorname{Im}(z'_2) \cdot i = 5 - 2i $$

Esta correspondencia biyectiva además preserva la suma. Por ejemplo:

$$ z_1 + z_2 = (3 + 4i) + (5 - 2i) = 8 + 2i $$

$$ (z_1 + z_2)' = \operatorname{Re}(z_1 + z_2) - \operatorname{Im}(z_1 + z_2) \cdot i = 8 - 2i $$

$$ z_1 + z_2 = \operatorname{Re}[(z_1 + z_2)'] - \operatorname{Im}[(z_1 + z_2)'] \cdot i = 8 + 2i $$

Asimismo, la correspondencia respeta el producto:

$$ z_1 \cdot z_2 = (3 + 4i)(5 - 2i) = 15 - 6i + 20i - 8i^2 = 23 + 14i $$

$$ (z_1 \cdot z_2)' = \operatorname{Re}(z_1 \cdot z_2) - \operatorname{Im}(z_1 \cdot z_2) \cdot i = 23 - 14i $$

$$ z_1 \cdot z_2 = \operatorname{Re}[(z_1 \cdot z_2)'] - \operatorname{Im}[(z_1 \cdot z_2)'] \cdot i = 23 + 14i $$

Y así sucesivamente.