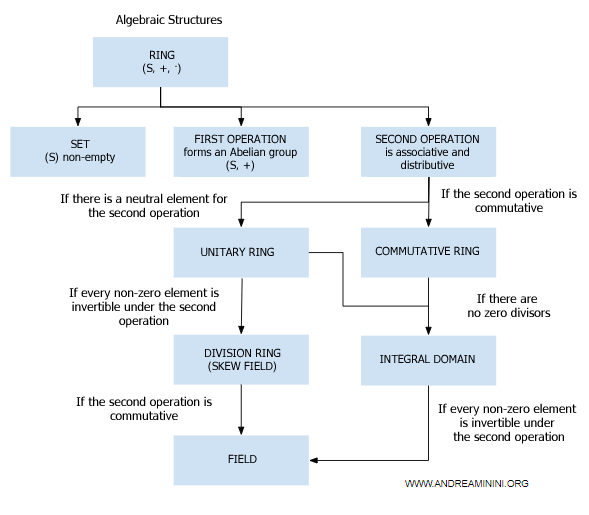
Dominios de integridad
Un dominio de integridad es un anillo (S, +, ·) conmutativo y unitario que no posee divisores de cero. $$ \forall \ a, b \in S \ , \ ab=0\ \Rightarrow\ (a=0\ \lor\ b=0) $$
En otras palabras, un dominio de integridad es un anillo conmutativo en el que el producto de dos elementos solo puede ser cero si al menos uno de ellos es cero.
Para comprobar si un anillo conmutativo (S, +, ·) es un dominio de integridad, es necesario demostrar que en el conjunto S no existen divisores de cero.
¿Qué es un divisor de cero? En un anillo conmutativo (S, +, ·), un elemento no nulo a ≠ 0 de S se denomina divisor de cero si existe otro elemento b ≠ 0 en S tal que ab = 0.
Un ejemplo práctico
El conjunto de los números enteros Z constituye un anillo (Z, +, ·) con las operaciones habituales de suma y producto.
$$ (Z,+,\cdot) $$
Se trata de un anillo conmutativo, ya que la multiplicación de enteros es conmutativa.
El producto de dos enteros no nulos a ≠ 0 y b ≠ 0 es siempre distinto de cero.
$$ \forall \ a,b \in Z \ , \ a \ne 0 \ , \ b \ne 0 \ \ \Longrightarrow \ \ ab \ne 0 $$
Nota. Si dos enteros tienen el mismo signo (ambos positivos o ambos negativos), su producto es positivo. Si tienen signos opuestos, el producto es negativo. Por tanto, si el producto de dos enteros es cero $$ ab = 0 $$ necesariamente al menos uno de los factores es cero. $$ a \cdot 0 = 0 \cdot a = 0 $$
En consecuencia, no existen divisores de cero en el conjunto Z.
Por lo tanto, el anillo conmutativo (Z, +, ·) es un dominio de integridad.
Ejemplo 2
Consideremos ahora el conjunto de clases de residuos módulo 6:
$$ Z_6 = \{ 0,1,2,3,4,5 \} $$
El conjunto Z6 forma un anillo conmutativo (Z6, +, ·) con las operaciones de suma (+) y producto (·) módulo 6.
$$ (Z_6,+, \cdot) $$
Para determinar si existen divisores de cero, podemos construir la tabla de multiplicación del anillo.
| a ·6 b | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 |
| 2 | 0 | 2 | 4 | 0 | 2 | 4 |
| 3 | 0 | 3 | 0 | 3 | 0 | 3 |
| 4 | 0 | 4 | 2 | 0 | 4 | 2 |
| 5 | 0 | 5 | 4 | 3 | 2 | 1 |
En este caso, hay tres divisores de cero: los números 2, 3 y 4.
Por ejemplo, el producto 2·3 es igual a cero porque el residuo es cero.
$$ 2 \cdot 3 \equiv 0 \ \text{mod} \ 6 $$
Explicación. Para calcular el producto de 2 por 3: $$ 2 \cdot 3 = 6 $$ A continuación se obtiene el residuo al dividir el resultado (2·3 = 6) entre 6: $$ 6 \div 6 = 1 \ \text{residuo} = 0 $$ El residuo es cero, por lo que en el sistema módulo 6 se tiene que 2·3 = 0. Lo mismo ocurre con el producto 3·2 = 0.
Por tanto, al existir divisores de cero, el anillo conmutativo (Z6, +, ·) no es un dominio de integridad.
En general, un anillo conmutativo Zn es un dominio de integridad únicamente cuando el número de elementos (n) es un número primo.
Ejemplo 3
Veamos ahora el conjunto de clases de residuos módulo 7:
$$ Z_7 = \{ 0,1,2,3,4,5,6 \} $$
En este caso, el número de elementos es un número primo (n = 7).
El conjunto Z7 constituye un anillo conmutativo (Z7, +, ·) con las operaciones de suma (+) y producto (·) definidas módulo 7.
$$ (Z_7,+, \cdot) $$
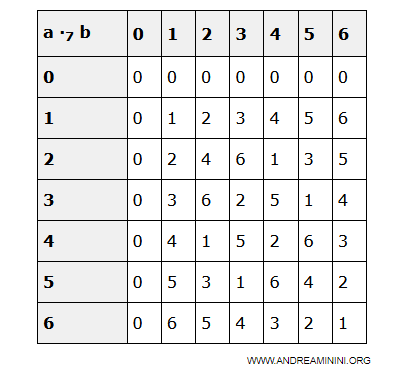
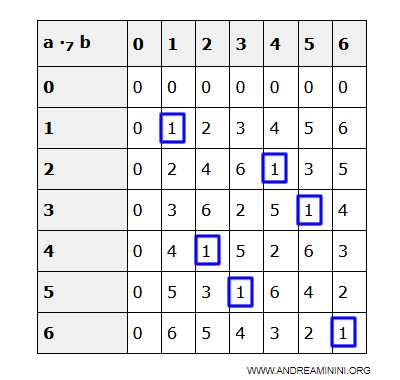
Construyamos la tabla de multiplicación para verificar si existen divisores de cero.
| a ·7 b | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 2 | 0 | 2 | 4 | 6 | 1 | 3 | 5 |
| 3 | 0 | 3 | 6 | 2 | 5 | 1 | 4 |
| 4 | 0 | 4 | 1 | 5 | 2 | 6 | 3 |
| 5 | 0 | 5 | 3 | 1 | 6 | 4 | 2 |
| 6 | 0 | 6 | 5 | 4 | 3 | 2 | 1 |
En este caso, no se encuentran divisores de cero.
Por lo tanto, el anillo conmutativo (Z7, +, ·) es un dominio de integridad.
Observaciones
Algunos puntos clave sobre los dominios de integridad:
-
Si todo elemento no nulo posee inverso multiplicativo (segunda operación), el dominio de integridad es un cuerpo.
- Todo dominio de integridad finito es un cuerpo
Un dominio de integridad finito se convierte en cuerpo si todos sus elementos no nulos son invertibles respecto al producto.
Demostración. Sea (D, +, ·) un dominio de integridad con un número finito n de elementos: $$ D = \{ a_1, a_2, ..., a_n \} $$ Es importante señalar que todos los elementos son distintos.
Ejemplo. Consideremos el conjunto Z7: $$ D = \{ 0,1,2,3,4,5,6 \} $$ que es un dominio de integridad (Z7, +, ·).
Tomemos un elemento no nulo ak de D $$ a_k \ne 0 $$ y consideremos la función que asocia ak con el producto de ak por cada elemento de D: $$ f: a_i \mapsto a_k \cdot a_i $$ Como el dominio es de integridad, los productos son todos distintos, por lo que la función f es inyectiva. Al ser D finito, f es también sobreyectiva.
Ejemplo. Si elegimos ak = 5 en Z7, los productos de 5 con los elementos de Z7 son todos distintos:
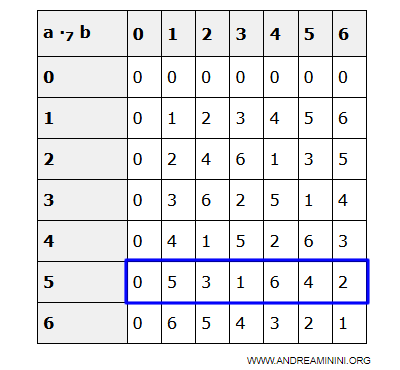
Esto implica que existe un elemento a0 en D tal que: $$ a_k \cdot a_0 = 1 $$ es decir, ak es invertible.
Ejemplo. En Z7, si ak = 5, entonces a0 = 3, ya que: $$ 5 \cdot 3 = 1 $$
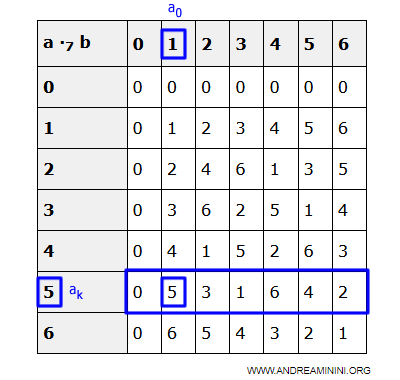
Por tanto, cualquier elemento x de D puede expresarse como: $$ x = a_k \cdot a_i $$
Ejemplo. Observando la tabla de multiplicación de Z7, el elemento 5 genera todos los elementos de Z7 al multiplicarse por los demás:
$$ 5 \cdot 0 = 0 \\ 5 \cdot 1 = 5 \\ 5 \cdot 2 = 3 \\ 5 \cdot 3 = 1 \\ 5 \cdot 4 = 6 \\ 5 \cdot 5 = 4 \\ 5 \cdot 6 = 2 $$Dado que: $$ x = a_0 \cdot x $$ y como la multiplicación en D es conmutativa y asociativa, se concluye que: $$ a_0 = 1 $$ es el elemento neutro para el producto en D.
De este modo, se demuestra la existencia de un elemento neutro y de inversos multiplicativos en D.
Ejemplo. En Z7, todos los elementos no nulos son invertibles. Por ejemplo: el inverso de 1 es 1; el de 2 es 4; el de 3 es 5; el de 4 es 2; el de 5 es 3; y el de 6 es 6.
En conclusión, el dominio de integridad (D, +, ·) es un cuerpo.
Y así sucesivamente.