Cuerpo de división (cuerpo no conmutativo)

En un cuerpo de división debe existir un elemento neutro para la multiplicación tal que:

$$ a \cdot 1 = a \ \ \ \ \ \forall \ a \in R $$

Asimismo, para cada elemento que no sea el neutro aditivo (cero), debe existir un inverso multiplicativo:

$$ a \cdot a^{-1} = 1 \ \ \ \ \ \forall \ a \ , \ a \ne 0 \ \ \in R $$

Esto significa que, en un cuerpo de división, el conjunto S junto con la operación de multiplicación constituye un grupo (S,·).

Nota: Aunque hablamos de "suma" y "multiplicación", en otros contextos estas operaciones pueden representar funciones distintas.

Es importante señalar que la multiplicación no tiene por qué ser conmutativa.

Si, en cambio, la multiplicación es conmutativa, el cuerpo de división se denomina cuerpo conmutativo o simplemente un cuerpo.

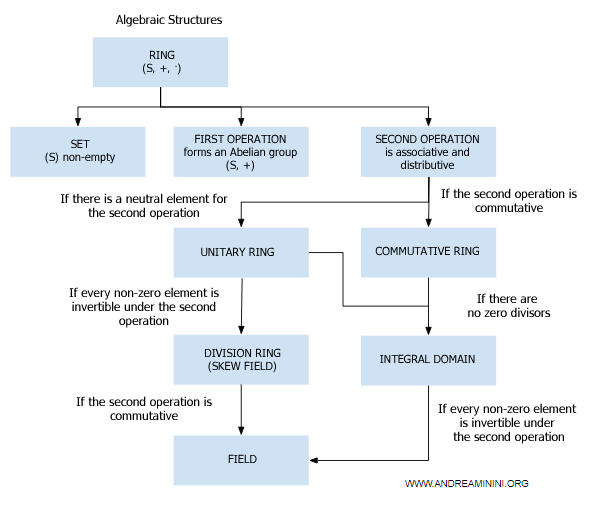
Un ejemplo práctico

Consideremos el conjunto de los números reales, R, con las operaciones de suma (+) y multiplicación (·):

$$ (R, + , \cdot ) $$

Para determinar si esta estructura algebraica es un cuerpo de división, debemos verificar si ambas operaciones cumplen con las propiedades necesarias.

Primera operación (+)

Comenzamos verificando si la suma define un grupo abeliano (R,+).

• La suma es cerrada en R: la suma de dos elementos cualesquiera a, b ∈ R también pertenece a R. $$ \forall \ a,b \in R \ \ \ \ a+b \in R $$
• La suma es asociativa: $$ \forall \ a,b,c \in R \ \ \ (a+b)+c = a+(b+c) $$
• Existe un elemento neutro para la suma: $$ \forall \ a \in R \ \ \ a + 0 = 0 + a = a $$
• Todo elemento de R posee un inverso aditivo: $$ \forall \ a \in R \ \ \ a + (-a) = (-a) + a = 0 $$

Por lo tanto, la operación de suma define un grupo (R,+) sobre los números reales.

Además, como la suma es conmutativa en R, este grupo es un grupo abeliano:

$$ \forall \ a,b \in R \ \ \ a+b = b+a $$

Así pues, la primera operación (+) cumple con todos los requisitos de un cuerpo de división.

Segunda operación (·)

Veamos ahora si la multiplicación en R satisface las condiciones necesarias:

• La multiplicación es cerrada en R: el producto de dos elementos cualesquiera a, b ∈ R también pertenece a R. $$ \forall \ a,b \in R\ \ \ \ a \cdot b \in R $$
• La multiplicación es distributiva con respecto a la suma, tanto por la izquierda como por la derecha: $$ \forall \ a,b,c \in R \ \ \ \ a \cdot (b+c) = ab + ac $$ $$ \forall \ a,b,c \in R \ \ \ \ (a+b) \cdot c = ac + bc $$
• La multiplicación es asociativa: $$ \forall \ a,b,c \in R \ \ \ (a \cdot b) \cdot c = a \cdot (b \cdot c) $$
• Existe un elemento neutro para la multiplicación: $$ \forall \ a \in R \ \ \ a \cdot 1 = 1 \cdot a = a $$
• Todo elemento distinto de cero en R posee un inverso multiplicativo: $$ \forall \ a \in R \ , \ a \ne 0 \ \ \ a \cdot a^{-1} = a^{-1} \cdot a = 1 $$

La segunda operación (·) cumple, por tanto, con todas las condiciones requeridas.

En conclusión, el anillo (R,+,·) es un cuerpo de división.

Nota: En este caso concreto, como la multiplicación es conmutativa, se trata en realidad de un cuerpo.

Y así sucesivamente.