Groupoides

¿Qué es un groupoide?

Un groupoide (o magma) es una estructura algebraica definida por un conjunto no vacío S y una operación binaria cerrada S×S→S.

En álgebra abstracta, el groupoide representa la estructura más elemental a partir de la cual se construyen todas las demás.

Al incorporar axiomas adicionales, es posible derivar distintas estructuras algebraicas a partir de los groupoides.

Nota: Si la operación de un groupoide es la suma, se denomina groupoide aditivo (S,+). Si la operación es el producto, hablamos de un groupoide multiplicativo (S,*).

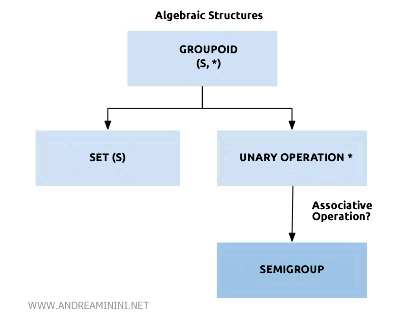
Cuando la operación de un groupoide también satisface la propiedad asociativa, se obtiene un pseudogrupo o un semigrupo.

Si además existe un elemento inverso para cada elemento del conjunto, entonces estamos ante un cuasigrupo.

Un ejemplo práctico

Ejemplo 1

La estructura (N,+) es un ejemplo de groupoide.

Está compuesta por el conjunto de los números naturales N y la operación de suma (+).

Dados dos elementos cualesquiera de N, su suma sigue perteneciendo a N:

$$ a+b \ \in N \ \ \ \ \ \ \forall \ a,b \in N $$

Por tanto, la operación de suma (+) es una operación cerrada en el conjunto de los números naturales N.

Nota: Otro ejemplo de groupoide es la estructura (N,*), ya que la multiplicación también es una operación cerrada en los números naturales.

Ejemplo 2

La estructura (N,-) no constituye un groupoide, ya que la resta no es una operación interna en el conjunto de los números naturales.

Por ejemplo:

$$ 4 - 5 = -1 \notin N $$

Nota: Sin embargo, la resta sí define un groupoide en el conjunto de los números enteros (Z,-), ya que en este caso la operación es cerrada.

Y así sucesivamente.