Semigrupos

¿Qué es un semigrupo?

Un semigrupo es una estructura algebraica (S,*) formada por un conjunto S y una operación binaria S×S→S, llamada operación de composición. Dicha operación satisface la propiedad asociativa, es decir: $$ (a*b)*c = a*(b*c) \ \ \ \forall \ a, b, c \ \in S $$

También se lo conoce como pseudogrupo.

En un semigrupo no se requiere la existencia de un elemento neutro ni de elementos inversos.

Si además el semigrupo incluye un elemento neutro, se denomina monoide.

Ejemplo

Consideremos, por ejemplo, el conjunto de los números naturales N con la operación de suma +.

$$ (N, +) $$

Esta estructura constituye un groupoide, ya que posee una operación binaria interna.

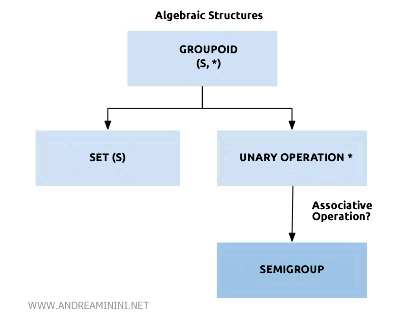
Además, es un semigrupo, puesto que la operación de suma es asociativa.

Para cualesquiera tres números naturales a, b y c, se cumple la propiedad asociativa:

$$ a + (b + c) = (a + b) + c $$

Por ejemplo, si a = 2, b = 3, c = 4:

$$ 2 + (3 + 4) = (2 + 3) + 4 = 9 $$

Y así sucesivamente.