Cuasigrupos
Un cuasigrupo es un groupoide (S,*) en el que, para cada par de elementos a y b, existen un inverso por la derecha (dx) y un inverso por la izquierda (sx) que satisfacen las siguientes ecuaciones: $$ a * d_x = b $$ y $$ s_x * a = b $$
Los cuasigrupos forman parte de una categoría más amplia dentro de los groupoides.
Es decir, todo cuasigrupo es un groupoide, aunque los inversos no son necesariamente conmutativos.
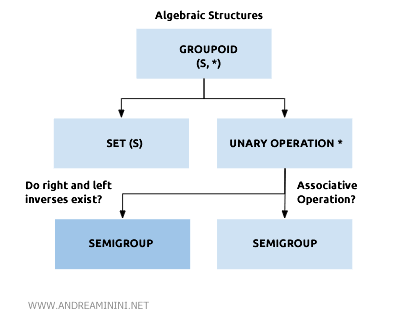
Si además el cuasigrupo posee un elemento neutro para la operación, se denomina loop.
Ejemplo aplicado
El conjunto de los números enteros Z con la operación de resta (-) constituye un cuasigrupo: $$ (Z,-) $$
Analicemos las propiedades de esta estructura algebraica.
La resta es una operación cerrada en el conjunto de los enteros Z, ya que la diferencia entre dos enteros siempre da como resultado otro entero:
$$ \forall a, b \in Z \Longrightarrow a - b \in Z $$
Por lo tanto, la estructura (Z,-) es un groupoide.
Ejemplo: Si tomamos a = 4 y b = 7, entonces: $$ a - b = 4 - 7 = -3 $$ que es un número entero.
Para cualquier par de enteros a y b, existen tanto un inverso por la derecha como uno por la izquierda.
Por consiguiente, la estructura (Z,-) es un cuasigrupo.
Ejemplo: Si a = 4 y b = 7, el inverso por la derecha x = -3 verifica: $$ a - x = b $$ $$ 4 - x = 7 $$ $$ x = 4 - 7 $$ $$ x = -3 $$ mientras que el inverso por la izquierda y = 11 satisface: $$ y - a = b $$ $$ y - 4 = 7 $$ $$ y = 7 + 4 $$ $$ y = 11 $$
Y así sucesivamente.