Loop en álgebra abstracta

Un loop es un tipo particular de cuasigrupo (S,*) que posee un elemento neutro que satisface las igualdades $$ a*x = a $$ y $$ x*a = a $$ para todo elemento \(a\) perteneciente a S.

Como ocurre en todo cuasigrupo, la estructura algebraica (S,*) exige que, dados cualesquiera elementos \(a\) y \(b\), existan elementos únicos que actúen como inversos por la izquierda y por la derecha, es decir:

$$ a*d_x = b $$ $$ s_x*a = b $$

Lo que caracteriza a los loops frente a los cuasigrupos generales es precisamente la existencia de un elemento neutro (e).

En un loop, para cada par de elementos \(a\) y \(b\), existe un único elemento \(x\) en S que satisface simultáneamente:

$$ a*x = b $$ $$ x*a = b $$

Los loops forman parte del conjunto más amplio de las estructuras grupoides.

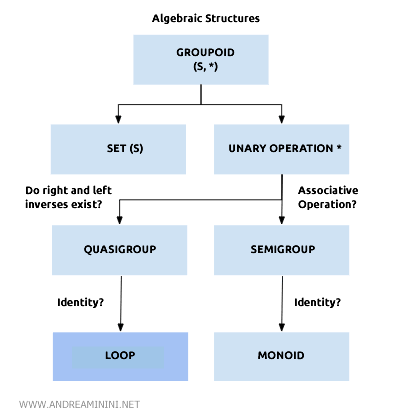
Cuando la operación * en un loop también es asociativa, la estructura resultante se denomina loop asociativo o simplemente un grupo.

Un ejemplo práctico

El conjunto de los números racionales distintos de cero, Q - {0}, con la operación multiplicación (·), forma un loop: (Q - {0},·).

$$ (Q - \{ 0 \}, \cdot) $$

Al analizar las propiedades de esta estructura algebraica, observamos que:

La multiplicación está cerrada en el conjunto Q - {0}, lo que significa que:

$$ \forall a, b \in Q - \{ 0 \} \Longrightarrow a \cdot b \in Q - \{ 0 \} $$

Por tanto, la estructura (Q - {0},·) cumple con los requisitos de un grupoide.

Ejemplo. Si tomamos los enteros a = 4 y b = 7, su producto también es un número racional: $$ a \cdot b = 4 \cdot 7 = 28 $$

Para cualquier par de enteros \(a\) y \(b\), se puede encontrar un elemento que actúe como inverso tanto por la izquierda como por la derecha.

En consecuencia, la estructura (Z,·) constituye un cuasigrupo.

Ejemplo. Sean a = 4 y b = 7. El elemento inverso \(x\) es \(7/4\): $$ a \cdot x = b $$ $$ 4 \cdot x = 7 $$ $$ x = \frac{7}{4} $$ y, recíprocamente, el mismo valor \(y = 7/4\): $$ y \cdot a = b $$ $$ y \cdot 4 = 7 $$ $$ y = \frac{7}{4} $$ Observa que los inversos por la izquierda y por la derecha coinciden.

En la estructura (Q - {0},·), existe un elemento neutro, que es el número \(e = 1\).

$$ \forall a \in Q - \{ 0 \} \Longrightarrow a \cdot 1 = 1 \cdot a = a $$

Por lo tanto, (Q - {0},·) es un loop.

Nota. Dado que la multiplicación es una operación asociativa, la estructura (Q - {0},·) no solo es un loop, sino que también es un loop asociativo, es decir, un grupo. En consecuencia, todo grupo es un loop, pero no todo loop es un grupo.

Y así sucesivamente.