Ecuación de una circunferencia que pasa por tres puntos no colineales

Para hallar la ecuación de una circunferencia que pase por tres puntos no colineales \( P(x_1, y_1) \), \( Q(x_2, y_2) \) y \( R(x_3, y_3) \), es necesario resolver el siguiente sistema de ecuaciones para determinar los coeficientes "a", "b" y "c": $$ \begin{cases} x_1^2 + y_1^2 + a x_1 + b y_1 + c = 0 \\ x_2^2 + y_2^2 + a x_2 + b y_2 + c = 0 \\ x_3^2 + y_3^2 + a x_3 + b y_3 + c = 0 \end{cases} $$ Una vez calculados los valores de "a", "b" y "c", se sustituyen en la ecuación general de la circunferencia: $$ x^2 + y^2 + ax + by + c = 0 $$

Ejemplo práctico

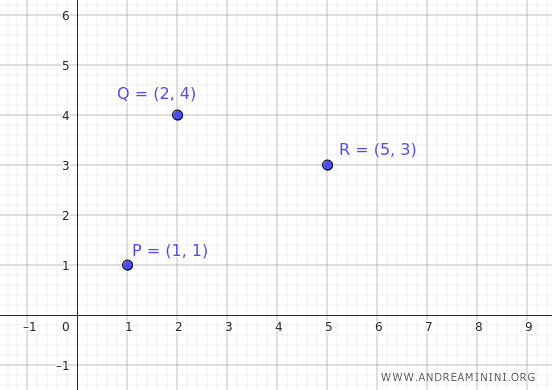
Consideremos los siguientes puntos en el plano:

$$ P(1, 1) $$

$$ Q(2, 4) $$

$$ R(5, 3) $$

Son tres puntos no colineales situados en el plano cartesiano.

La ecuación general de la circunferencia es:

$$ x^2 + y^2 + ax + by + c = 0 $$

Para resolver este ejercicio, seguimos los pasos que se indican a continuación:

1] Plantear las ecuaciones correspondientes a cada punto

Sustituimos las coordenadas de cada punto en la ecuación general:

• Para el punto P(1,1), sustituimos x=1 e y=1:
  $ x^2 + y^2 + ax + by + c = 0 $
  $ 1^2 + 1^2 + a \cdot 1 + b \cdot 1 + c = 0 $
  $ 1 + 1 + a + b + c = 0 $
  $ a + b + c = -2 $
• Para el punto Q(2, 4), sustituimos x=2 e y=4:
  $ x^2 + y^2 + ax + by + c = 0 $
  $ 2^2 + 4^2 + a \cdot 2 + b \cdot 4 + c = 0 $
  $ 4 + 16 + 2a + 4b + c = 0 $
  $ 2a + 4b + c = -20 $
• Para el punto R(5, 3), sustituimos x=5 e y=3:
  $ x^2 + y^2 + ax + by + c = 0 $
  $ 5^2 + 3^2 + a \cdot 5 + b \cdot 3 + c = 0 $
  $ 25 + 9 + 5a + 3b + c = 0 $
  $ 5a + 3b + c = -34 $

2] Plantear y resolver el sistema de ecuaciones

Reunimos las tres ecuaciones en el siguiente sistema lineal:

$$ \begin{cases} a + b + c = -2 \\ 2a + 4b + c = -20 \\ 5a + 3b + c = -34 \\ \end{cases} $$

Este sistema nos permite determinar los valores de los coeficientes "a", "b" y "c" que definen la circunferencia que pasa por los tres puntos.

Procedemos a resolverlo utilizando el método de reducción.

Restamos la primera ecuación de la segunda:

$$ \begin{cases} a + b + c = -2 \\ (2a + 4b + c) - (a + b + c) = -20 - (-2) \\ 5a + 3b + c = -34 \\ \end{cases} $$

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ 5a + 3b + c = -34 \\ \end{cases} $$

Restamos la primera ecuación de la tercera:

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ (5a + 3b + c) - (a + b + c) = -34 - (-2) \\ \end{cases} $$

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ 4a + 2b = -32 \\ \end{cases} $$

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ 2a + b = -16 \\ \end{cases} $$

Eliminamos la variable "c" y trabajamos solo con las dos últimas ecuaciones para obtener "a" y "b".

Multiplicamos la tercera ecuación por 3:

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ 3 \cdot (2a + b) = 3 \cdot ( -16) \\ \end{cases} $$

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ 6a + 3b = -48 \\ \end{cases} $$

Restamos la segunda ecuación de la tercera para eliminar "b":

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ 6a + 3b - (a + 3b) = -48 - (-18) \\ \end{cases} $$

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ (6a - a) + (3b - 3b) = -48 + 18 \\ \end{cases} $$

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ 5a = -30 \\ \end{cases} $$

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ a = - \frac{30}{5} \\ \end{cases} $$

$$ \begin{cases} a + b + c = -2 \\ a + 3b = -18 \\ a = - 6 \\ \end{cases} $$

Con \( a = -6 \), sustituimos este valor en las ecuaciones anteriores para hallar "b" y "c":

$$ \begin{cases} -6 + b + c = -2 \\ -6 + 3b = -18 \\ a = - 6 \\ \end{cases} $$

$$ \begin{cases} b + c = -2 + 6 \\ 3b = -18 + 6 \\ a = - 6 \\ \end{cases} $$

$$ \begin{cases} b + c = 4 \\ b = - \frac{12}{3} \\ a = - 6 \\ \end{cases} $$

$$ \begin{cases} b + c = 4 \\ b = - 4 \\ a = - 6 \\ \end{cases} $$

Conocemos ahora \( b = -4 \). Sustituimos este valor en la primera ecuación para determinar "c":

$$ \begin{cases} -4 + c = 4 \\ b = - 4 \\ a = - 6 \\ \end{cases} $$

$$ \begin{cases} c = 4 + 4 \\ b = - 4 \\ a = - 6 \\ \end{cases} $$

$$ \begin{cases} c = 8 \\ b = - 4 \\ a = - 6 \\ \end{cases} $$

3] Escribir la ecuación de la circunferencia que pasa por los tres puntos

Finalmente, hemos hallado los valores de los tres coeficientes: a = -6, b = -4 y c = 8.

Por tanto, la ecuación de la circunferencia que pasa por los puntos P, Q y R es:

$$ x^2 + y^2 + ax + by + c = 0 $$

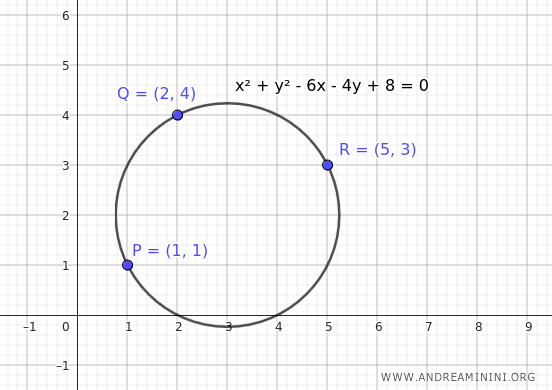
$$ x^2 + y^2 - 6x - 4y + 8 = 0 $$

A continuación, se muestra la representación gráfica de la circunferencia:

Demostración

La ecuación de la circunferencia se expresa en la forma:

$$ x^2 + y^2 + ax + by + c = 0 $$

Para garantizar que la circunferencia pase por los puntos \( P \), \( Q \) y \( R \), es imprescindible que las coordenadas de estos puntos satisfagan dicha ecuación.

• Punto P(x₁,y₁): $$ x_1^2 + y_1^2 + a x_1 + b y_1 + c = 0 $$
• Punto Q(x₂,y₂): $$ x_2^2 + y_2^2 + a x_2 + b y_2 + c = 0 $$
• Punto R(x₃,y₃): $$ x_3^2 + y_3^2 + a x_3 + b y_3 + c = 0 $$

Observamos que los coeficientes "a", "b" y "c" son comunes en todas las ecuaciones.

Así, podemos plantear el siguiente sistema de ecuaciones:

$$ \begin{cases} x_1^2 + y_1^2 + a x_1 + b y_1 + c = 0 \\ x_2^2 + y_2^2 + a x_2 + b y_2 + c = 0 \\ x_3^2 + y_3^2 + a x_3 + b y_3 + c = 0 \\ \end{cases} $$

En este punto, basta resolver dicho sistema para obtener los valores de \( a \), \( b \) y \( c \), que determinan por completo la ecuación de la circunferencia que pasa por los tres puntos dados.

Una vez hallados, se sustituyen en la ecuación general de la circunferencia:

$$ x^2 + y^2 + ax + by + c = 0 $$

Y con ello se concluye el proceso.