Cómo deducir la ecuación de una circunferencia a partir de su radio y su centro
La ecuación de una circunferencia en el plano cartesiano se puede obtener si conocemos el radio (r) y las coordenadas de su centro, C(x0, y0). La fórmula es: $$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$
Esta ecuación describe todos los puntos \((x, y)\) que se encuentran a una distancia \(r\) del centro \((x_0, y_0)\).
Ejemplo práctico
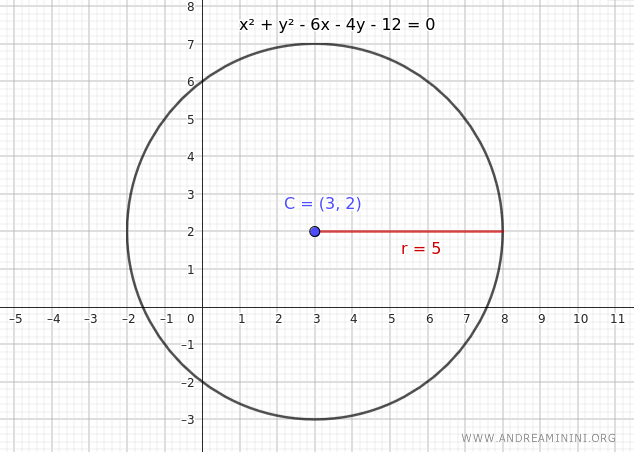
Vamos a estudiar una circunferencia cuyo centro está en \( C(3, 2) \) y cuyo radio es \( r = 5 \).
Para determinar su ecuación, utilizamos la fórmula:
$$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$
En este caso, las coordenadas del centro son x0=3 y y0=2, y el radio es r=5.
$$ (x - 3)^2 + (y - 2)^2 = 5^2 $$
$$ (x - 3)^2 + (y - 2)^2 = 25 $$
La ecuación \((x - 3)^2 + (y - 2)^2 = 25\) representa todos los puntos \((x, y)\) que se hallan a 5 unidades de distancia del centro \((3, 2)\).
Si queremos expresar esta ecuación en su forma general, desarrollamos los binomios:
$$ (x - 3)^2 + (y - 2)^2 = 25 $$
$$ x^2 - 6x + 9 + y^2 - 4y + 4 - 25 = 0 $$
$$ x^2 + y^2 - 6x - 4y - 12 = 0 $$
Este es un ejemplo concreto de cómo encontrar la ecuación de una circunferencia conociendo su centro y su radio.
Nota: Para verificar si un punto pertenece a la circunferencia, basta sustituir las coordenadas del punto en la ecuación y comprobar si se cumple la igualdad. Por ejemplo, para saber si el punto P(6,6) está sobre la circunferencia, sustituimos x=6 e y=6 en la ecuación. $$ (x - 3)^2 + (y - 2)^2 = 25 $$ $$ (6 - 3)^2 + (6 - 2)^2 = 25 $$ $$ 3^2 + 4^2 = 25 $$ $$ 9 + 16 = 25 $$ $$ 25 = 25 $$ Dado que la distancia coincide con el radio, el punto (6,6) se encuentra sobre la circunferencia, lo que confirma que la ecuación es correcta. Otra opción es sustituir x=6 e y=6 en la ecuación general de la circunferencia. El resultado es el mismo. $$ x^2 + y^2 - 6x - 4y - 12 = 0 $$ $$ 6^2 + 6^2 - 6 \cdot 6 - 4 \cdot 6 - 12 = 0 $$ $$ 36 + 36 - 36 - 24 - 12 = 0 $$ $$ 0 = 0 $$
La demostración
Para empezar, conocemos el centro de la circunferencia: \(C(x_0, y_0)\) y su radio: \(r\).
Queremos demostrar que la ecuación de la circunferencia en el plano cartesiano es \((x - x_0)^2 + (y - y_0)^2 = r^2\).
Por definición, una circunferencia es el conjunto de todos los puntos de un plano que se encuentran a la misma distancia de un punto fijo llamado centro. Esa distancia constante es el radio \(r\).
Así, si tomamos un punto cualquiera \(P(x, y)\) sobre la circunferencia, la distancia entre \(P(x, y)\) y el centro \(C(x_0, y_0)\) debe ser igual al radio \(r\).
La fórmula para calcular la distancia entre dos puntos \((x, y)\) y \((x_0, y_0)\) en el plano cartesiano es:
$$ d = \sqrt{(x - x_0)^2 + (y - y_0)^2} $$
En este caso, la distancia (d) debe ser igual al radio (r) de la circunferencia, es decir, d = r.
$$ \sqrt{(x - x_0)^2 + (y - y_0)^2} = r $$
Para eliminar la raíz cuadrada, elevamos ambos lados de la ecuación al cuadrado:
$$ (\sqrt{(x - x_0)^2 + (y - y_0)^2})^2 = r^2 $$
$$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$
Esta ecuación describe todos los puntos \((x, y)\) que se encuentran a una distancia \(r\) del centro \(C(x_0, y_0)\).
Por tanto, hemos demostrado la fórmula de la ecuación de una circunferencia, dada su centro \(C(x_0, y_0)\) y su radio \(r\).