Cómo deducir la ecuación de una circunferencia a partir de los extremos de su diámetro
Para determinar la ecuación de una circunferencia conociendo los extremos A y B de su diámetro, puedes seguir estos pasos:
- Calcular el centro de la circunferencia
El centro \( C \) se obtiene hallando el punto medio del segmento que une los puntos \( A \) y \( B \). Si \( A \) tiene coordenadas \((x_A, y_A)\) y \( B \) tiene coordenadas \((x_B, y_B)\), el centro \( C \) se calcula como: $$ \left( \frac{x_A + x_B}{2}, \frac{y_A + y_B}{2} \right) $$ - Determinar el radio
El radio \( r \) es la mitad de la distancia entre los puntos \( A \) y \( B \). Esta distancia se obtiene aplicando la fórmula de la distancia euclidiana: $$ AB = \sqrt{(x_A - x_B)^2 + (y_A - y_B)^2} $$ Por tanto, el radio \( r \) es: $$ r = \frac{1}{2} \cdot \sqrt{(x_A - x_B)^2 + (y_A - y_B)^2} $$ - Escribir la ecuación de la circunferencia
Una vez conocidos el centro \( C(x_0, y_0) \) y el radio \( r \), se puede expresar la ecuación en su forma ordinaria: $$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$ donde \( x_0 = \frac{x_A + x_B}{2} \) y \( y_0 = \frac{y_A + y_B}{2} \).
Ejemplo práctico
Veamos un ejemplo paso a paso para entender mejor el procedimiento.
Consideremos dos puntos \( A(2, 3) \) y \( B(8, 7) \), que son los extremos del diámetro de una circunferencia.
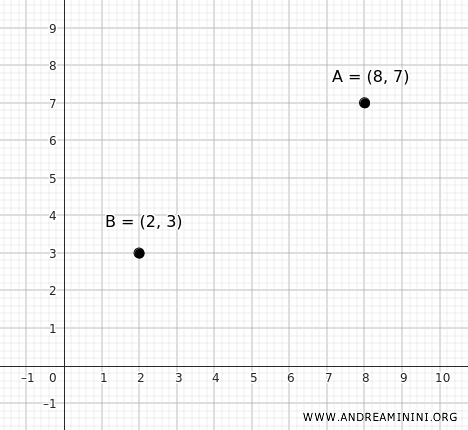
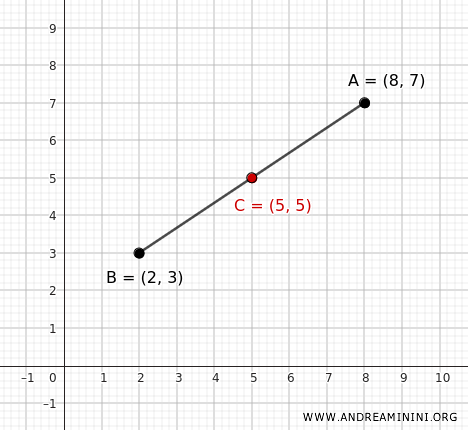
El centro \( C \) es el punto medio del segmento \( AB \):
$$ C \left( \frac{x_A + x_B}{2}, \frac{y_A + y_B}{2} \right) $$
$$ C \left( \frac{2 + 8}{2}, \frac{3 + 7}{2} \right) $$
$$ C \left( \frac{10}{2}, \frac{10}{2} \right) $$
$$ C(5, 5) $$
Por tanto, el centro de la circunferencia se encuentra en las coordenadas \( C(5, 5) \) del plano cartesiano.
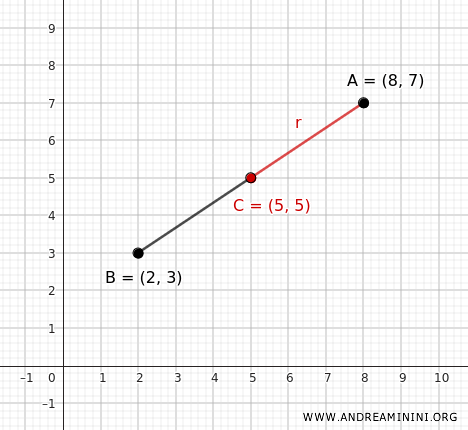
La distancia \( AB \) entre los puntos \( A \) y \( B \) se calcula mediante la fórmula de distancia euclidiana:
$$ AB = \sqrt{(x_A - x_B)^2 + (y_A - y_B)^2} $$
$$ AB = \sqrt{(2 - 8)^2 + (3 - 7)^2} $$
$$ AB = \sqrt{(-6)^2 + (-4)^2} $$
$$ AB = \sqrt{36 + 16} $$
$$ AB = \sqrt{52} $$
$$ AB = 2\sqrt{13} $$
Como el radio es la mitad del diámetro, dividimos la distancia \( AB \) entre dos:
$$ r = \frac{1}{2} \cdot AB $$
$$ r = \frac{1}{2} \cdot 2\sqrt{13} $$
$$ r = \sqrt{13} $$
Por lo tanto, el radio es \( r = \sqrt{13} \).
Ahora podemos escribir la ecuación de la circunferencia cuyo centro es \( C(5, 5) \) y cuyo radio es \( r = \sqrt{13} \).
La fórmula general de la circunferencia dada su centro y radio es la siguiente:
$$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$
En este caso, las coordenadas del centro son \( x_0 = 5 \) y \( y_0 = 5 \), por lo que la ecuación queda:
$$ (x - 5)^2 + (y - 5)^2 = (\sqrt{13})^2 $$
$$ (x - 5)^2 + (y - 5)^2 = 13 $$
Esta es la ecuación de la circunferencia cuyo diámetro tiene por extremos los puntos \( A(2, 3) \) y \( B(8, 7) \).
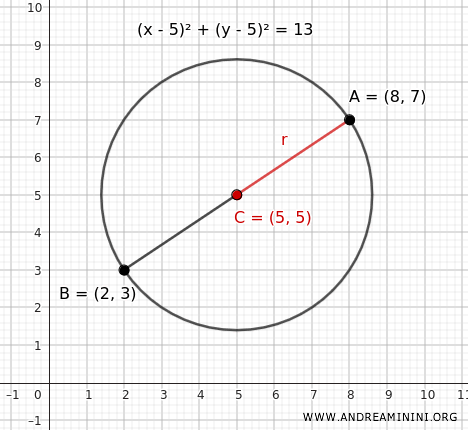
Y así es como se obtiene.