Teorema de las tres perpendiculares
Si desde un punto \( P \) situado sobre la recta \( r \) se trazan dos rectas \( a \) y \( b \), ambas perpendiculares a \( r \), entonces \( r \) es perpendicular a cualquier otra recta \( s \) que pase por \( P \) y se encuentre en el plano \( \alpha \) definido por \( a \) y \( b \).
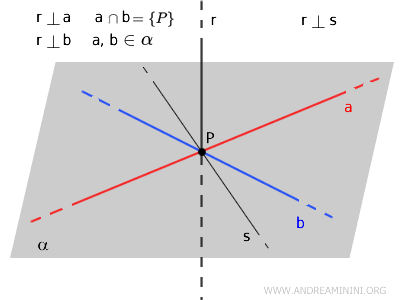
El teorema de las tres perpendiculares constituye una herramienta fundamental en geometría tridimensional, pues permite establecer relaciones de ortogonalidad entre rectas y planos de manera rigurosa.
Por ejemplo, ofrece un método eficaz para determinar si una recta es perpendicular a otra recta o a un plano, analizando las relaciones que mantienen dentro del plano involucrado.
Demostración
Consideremos un punto \( P \) y una recta \( r \).
Se trazan dos rectas \( a \) y \( b \), ambas perpendiculares a \( r \) y que pasan por \( P \).
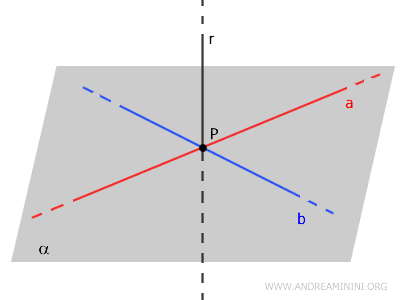
Las rectas \( a \) y \( b \) determinan el plano \( \alpha \), lo que implica que son coplanares.
Por construcción, \( a \) y \( b \) se intersectan en \( P \) y ambas son perpendiculares a \( r \).
$$ a \cap b = \{ P \} $$
$$ a, b \in \alpha $$
$$ a , b \perp r $$
En consecuencia, \( r \) es perpendicular al plano \( \alpha \), y su intersección se reduce al punto \( P \).
$$ r \cap \alpha = \{ P \} $$
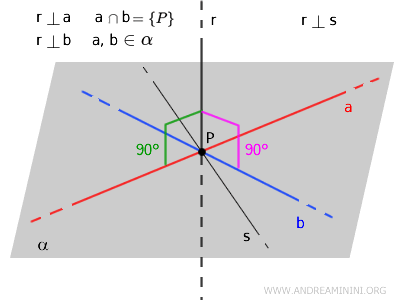
A continuación, se eligen dos puntos \( Q \) y \( R \) sobre \( r \), situados a la misma distancia de \( P \), pero en lados opuestos respecto al plano \( \alpha \).
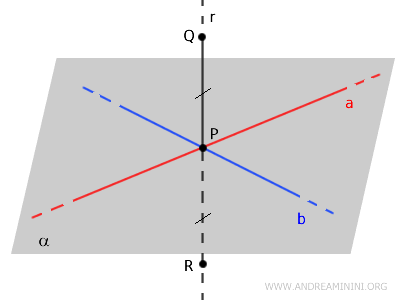
Como \( Q \) y \( R \) son equidistantes de \( P \), se tiene que los segmentos \( PQ \) y \( PR \) son congruentes:
$$ PQ \cong PR $$
Seguidamente, se traza una recta \( s \) contenida en el plano \( \alpha \).
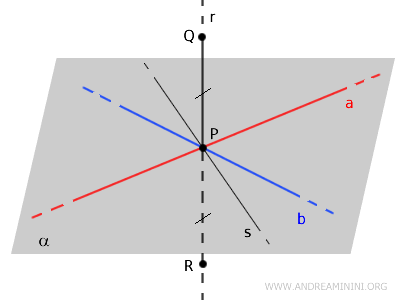
Se seleccionan dos puntos \( A \) y \( B \) sobre las rectas \( a \) y \( b \), respectivamente, y se los une mediante el segmento \( AB \), el cual corta a \( s \) en un punto \( T \).
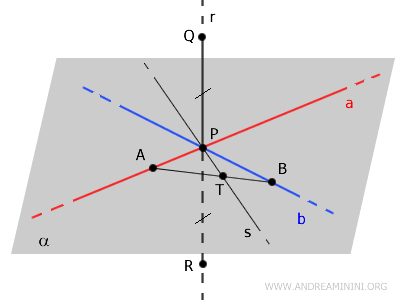
Se construyen los segmentos \( AQ, TQ, BQ \) y \( AR, TR, BR \), generando así diversos triángulos en el espacio.
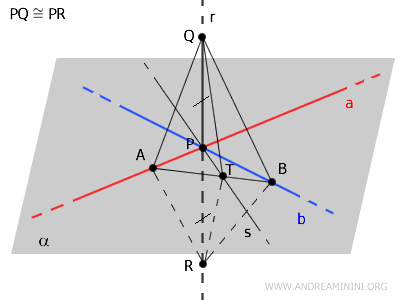
En el triángulo \( \triangle AQR \), el segmento \( AP \) funciona simultáneamente como altura y mediana relativa a la base \( QR \), ya que \( PQ \cong PR \).
Esto demuestra que \( \triangle AQR \) es un triángulo isósceles, por lo que \( AQ \cong AR \).
$$ PQ \cong PR $$
De manera análoga, el triángulo \( \triangle BQR \) también resulta isósceles, pues \( PB \) actúa tanto de altura como de mediana respecto a \( QR \).
Por lo tanto, \( BQ \cong BR \).
$$ BQ \cong BR $$
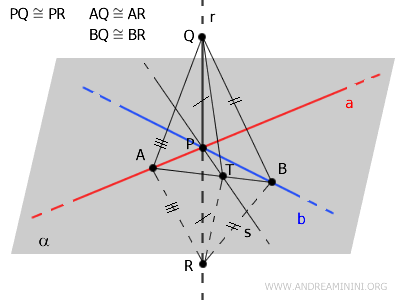
Consideremos ahora los triángulos \( \triangle ABQ \) y \( \triangle ABR \).
Según el tercer criterio de congruencia de triángulos, se cumple que \( \triangle ABQ \cong \triangle ABR \), pues comparten el lado \( AB \) y presentan dos pares de lados congruentes: \( AQ \cong AR \) y \( BQ \cong BR \).
$$ ABQ \cong ABR $$
La congruencia de estos triángulos implica que sus ángulos homólogos son iguales.
En particular, los ángulos \( \angle ABQ \) y \( \angle ABR \) resultan congruentes.
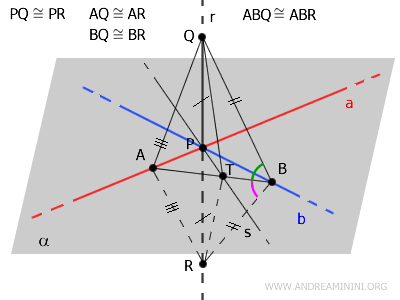
En los triángulos \( \triangle TBQ \) y \( \triangle TBR \), el lado \( TB \) es común, \( BQ \cong BR \), y los ángulos \( \angle ABQ \) y \( \angle ABR \) son congruentes.
Por el primer criterio de congruencia de triángulos, se concluye que \( \triangle TBQ \cong \triangle TBR \).
$$ TBQ \cong TBR $$
La congruencia de \( \triangle TBQ \) y \( \triangle TBR \) implica que todos sus lados correspondientes son iguales.
En particular, \( TQ \cong TR \).
$$ TQ \cong TR $$
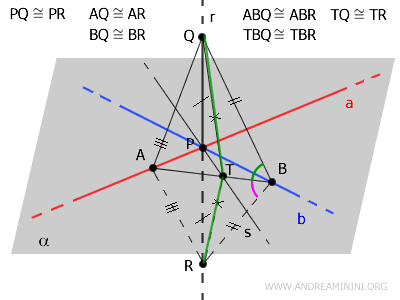
Con \( TQ \cong TR \), se concluye que el triángulo \( \triangle TQR \) es isósceles.
Por lo tanto, \( PT \) actúa simultáneamente como altura y mediana en \( \triangle TQR \).
Esto implica que \( PT \) es perpendicular a la base \( QR \), formando un ángulo recto de \( 90^\circ \).
$$ PT \perp QR $$
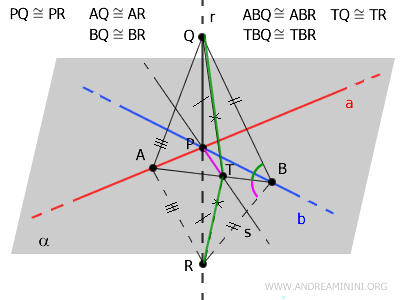
Finalmente, dado que \( QR \) pertenece a la recta \( r \) y \( PT \) pertenece a la recta \( s \), se concluye que las rectas \( r \) y \( s \) son perpendiculares.
$$ r \perp s $$
Este mismo razonamiento se aplica a cualquier recta \( s \) contenida en el plano \( \alpha \).

De este modo, el teorema queda demostrado.
Y así sucesivamente.