Teorema de las rectas perpendiculares a una recta en el espacio

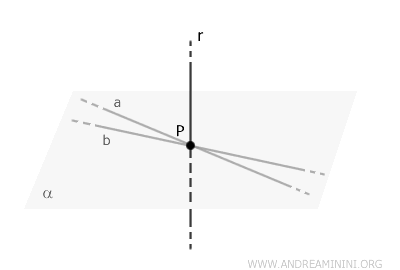
En el espacio, todas las rectas perpendiculares a una recta \( r \) que pasan por un punto \( P \in r \) se hallan contenidas en un único plano, \( \alpha \).

Demostración

Para demostrar que todas las rectas perpendiculares a \( r \) que pasan por \( P \) se encuentran en un mismo plano, recurriremos a un razonamiento por contradicción, que nos llevará a un resultado imposible.

Consideremos dos rectas \( a \) y \( b \), ambas perpendiculares a \( r \) y que pasan por \( P \).

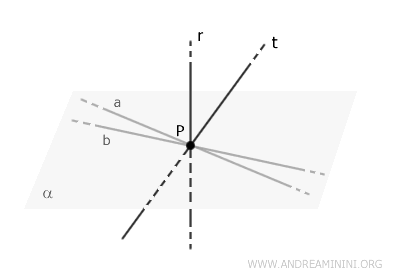
Estas dos rectas definen un plano, al que llamaremos \( \alpha \), que es también perpendicular a la recta \( r \). En consecuencia, \( \alpha \) contiene a \( a \) y \( b \).

Supongamos ahora, con el fin de alcanzar una contradicción, que existe otra recta \( t \), perpendicular a \( r \) y que pasa por \( P \), pero que no está contenida en el plano \( \alpha \).

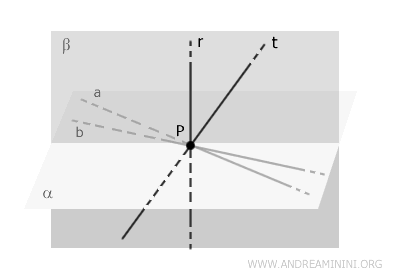
Si la recta \( t \) no se encuentra en \( \alpha \), necesariamente existe otro plano distinto, \( \beta \), determinado por las rectas \( t \) y \( r \).

Así, \( \beta \) es el plano que contiene simultáneamente a \( r \) y a \( t \).

Los planos \( \alpha \) y \( \beta \) se intersectan según una recta \( s \), que necesariamente pasa por el punto \( P \), ya que ambos planos contienen dicho punto.

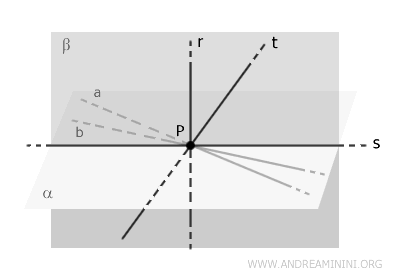
Sin embargo, esta situación conduce a una contradicción.

La recta \( s \), por ser intersección de los planos \( \alpha \) y \( \beta \), pertenece simultáneamente a ambos.

Como \( s \) está contenida en \( \alpha \), y este plano está definido por las rectas \( a \) y \( b \), ambas perpendiculares a \( r \), el teorema de las tres perpendiculares garantiza que \( s \) es también perpendicular a \( r \).

Así, en el plano \( \beta \) existirían dos rectas - \( t \) (por hipótesis) y \( s \) (por construcción) - perpendiculares a \( r \) y que pasan por \( P \). Esto es imposible, pues en un mismo plano sólo puede existir una única recta perpendicular a otra dada, que pase por un punto concreto.

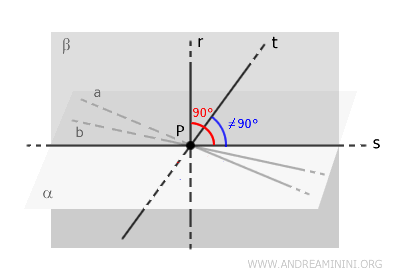
Por lo tanto, en el plano \( \beta \), que además contiene a la recta \( r \), no pueden coexistir dos rectas distintas perpendiculares a \( r \) que pasen por el mismo punto \( P \).

Dado que la suposición de que \( t \) no pertenece al plano \( \alpha \) lleva a una contradicción, debemos concluir necesariamente lo contrario: \( t \) está contenida en el plano \( \alpha \).

Queda así demostrado que todas las rectas perpendiculares a \( r \) y que pasan por un punto \( P \) sobre \( r \) se hallan contenidas en un único plano, \( \alpha \).

Y con esto, el teorema queda demostrado.

Y así sucesivamente.