Teorema de las tres perpendiculares
Si desde el punto \( H \), donde una recta \( r \) es perpendicular a un plano \( \alpha \), se traza una recta \( t \) perpendicular a otra recta \( s \) situada en dicho plano, entonces la recta \( s \) resulta perpendicular al plano \( \beta \), definido por las rectas \( r \) y \( t \).
Demostración
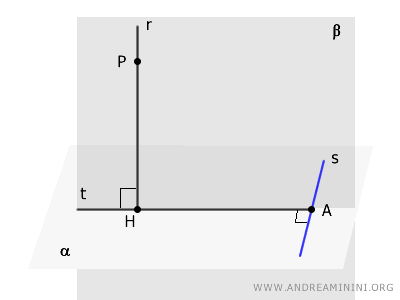
Sea un plano \( \alpha \) y una recta \( r \) perpendicular a él (\( r \perp \alpha \)), siendo \( H \) el pie de la perpendicular. Consideremos una recta \( s \) contenida en el plano \( \alpha \).

Se traza una recta \( t \), perpendicular a \( s \), que pasa por el punto \( H \) y corta a \( s \) en el punto \( A \).

Acto seguido, se elige un punto arbitrario \( P \) sobre la recta \( r \), y se traza el segmento \( PA \).

Se seleccionan ahora dos puntos \( B \) y \( C \) sobre la recta \( s \), equidistantes del punto \( A \), pero situados en lados opuestos respecto a él.
Así se obtienen dos segmentos congruentes: \( AB \cong AC \).

A continuación, se unen los puntos \( B \) y \( C \) con el punto \( H \).
Dado que \( H \) se halla sobre la mediatriz del segmento \( BC \), el triángulo \( BCH \) es isósceles, lo que implica que sus lados oblicuos son congruentes: \( BH \cong CH \).

Seguidamente, se conectan los puntos \( B \) y \( C \) con el punto \( P \) sobre la recta \( r \).
Los triángulos \( BPH \) y \( CPH \) resultan congruentes, ya que comparten el lado \( HP \), poseen lados congruentes \( BH \cong CH \), y contienen un ángulo recto idéntico (90°). De ello se sigue que los segmentos \( BP \cong CP \) son congruentes.

Por tanto, el triángulo \( BCP \) es isósceles, pues presenta dos lados iguales: \( BP \cong CP \).
En consecuencia, el segmento \( AP \) actúa simultáneamente como mediana, mediatriz y altura de dicho triángulo, lo cual implica que \( AP \) es perpendicular a la base \( BC \) del triángulo \( BCP \):
$$ AP \perp s $$
Por último, dado que \( s \) es perpendicular tanto a \( AH \) como a \( AP \), se concluye que \( s \) es perpendicular al plano \( \beta \), definido por los segmentos \( AH \) y \( AP \), el cual coincide con el plano determinado por las rectas \( r \) y \( t \).

Con esto, queda completada la demostración.