Teorema de las rectas perpendiculares

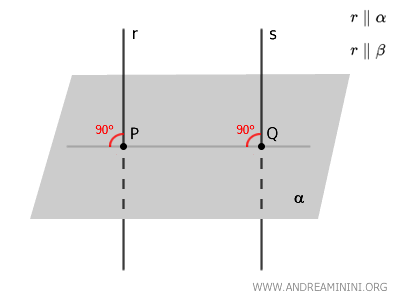
Si dos rectas \( r \) y \( s \) son perpendiculares a un mismo plano \( \alpha \), entonces dichas rectas son paralelas entre sí, es decir, \( r \parallel s \).

Demostración

Consideremos dos rectas \( r \) y \( s \) perpendiculares al plano \( \alpha \).

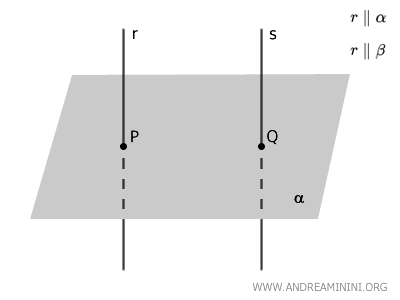
Los puntos \( P \) y \( Q \) son los pies de las perpendiculares trazadas desde \( r \) y \( s \) hacia el plano \( \alpha \).

$$ r \perp \alpha $$

$$ s \perp \alpha $$

Por definición, toda recta perpendicular a un plano forma un ángulo recto (\(90^\circ\)) con cualquier recta contenida en dicho plano.

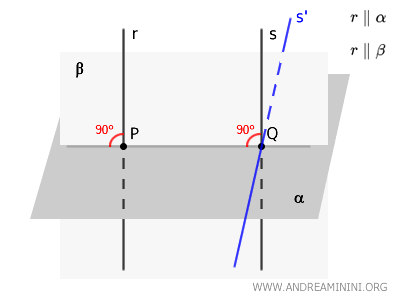
Por consiguiente, las rectas \( r \) y \( s \) han de formar ángulos rectos con la recta \( PQ \), la cual yace en el plano \( \alpha \) y une los puntos \( P \) y \( Q \), pies de las perpendiculares.

A continuación, utilizamos las rectas \( r \) y \( PQ \) para definir un nuevo plano \( \beta \).

Por construcción, \( r \) y \( PQ \) se encuentran en el mismo plano \( \beta \).

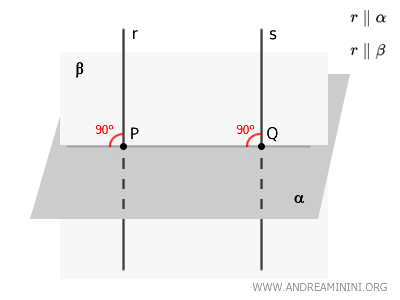
Supongamos ahora, por reducción al absurdo, que \( r \) y \( s \) no son paralelas y analicemos las consecuencias de esta hipótesis.

Si no fueran paralelas, entonces o bien se cortarían en algún punto, o bien formarían un ángulo distinto de \(90^\circ\) entre ellas.

En cualquiera de estos casos se llega a una contradicción:

• Si \( r \) y \( s \) se cortaran en el plano \( \beta \), necesariamente al menos una de ellas formaría un ángulo distinto de \(90^\circ\) con la recta \( PQ \). Esto contradiría el hecho de que \( r \) y \( s \) son perpendiculares a todas las rectas del plano \( \alpha \), incluida \( PQ \).
  
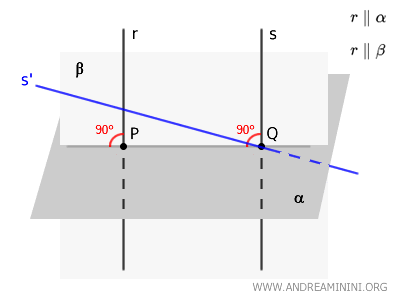
• Si \( r \) y \( s \) no se cortaran en \( \beta \) ni fueran paralelas, serían rectas alabeadas. En tal caso, al menos una de ellas debería formar un ángulo distinto de \(90^\circ\) con el plano \( \alpha \), lo cual contradice la hipótesis inicial de que ambas son perpendiculares a \( \alpha \).
  

Por tanto, la suposición de que \( r \) y \( s \) no son paralelas es falsa, pues conduce a una contradicción.

En consecuencia, se deduce que \( r \) y \( s \) deben ser paralelas.

Observaciones adicionales

A continuación, se presentan algunas observaciones y precisiones relacionadas con este teorema:

• Teorema de las rectas perpendiculares a otra recta en el espacio
  En el espacio tridimensional (3D), el teorema que afirma que dos rectas perpendiculares a una misma recta son paralelas no siempre se cumple. Este principio sólo es válido en el plano (2D), donde las restricciones geométricas son más estrictas.
  
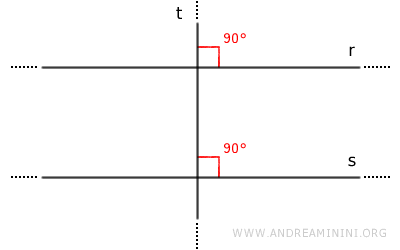
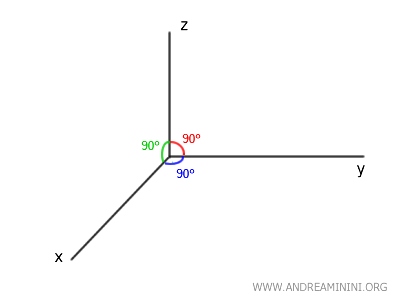
  ¿Por qué este teorema es válido en el plano pero no en el espacio 3D? En un plano bidimensional, dos rectas perpendiculares a una misma recta deben ser paralelas, pues no existe otra dirección en la que puedan desviarse. La perpendicularidad respecto a la misma recta obliga a que ambas sigan trayectorias paralelas. En cambio, en el espacio tridimensional, dos rectas perpendiculares a una misma recta pueden pertenecer a planos distintos sin ser necesariamente paralelas. Esto se debe a la mayor libertad de orientación en el espacio, donde una recta puede inclinarse en múltiples direcciones y seguir siendo perpendicular a la misma recta de referencia.

  Ejemplo: En un sistema de coordenadas cartesianas tridimensional, los ejes cartesianos (\(x\)-\(y\)-\(z\)) son mutuamente perpendiculares, formando ángulos rectos (\(90^\circ\)) entre sí:
  - El eje \(x\) es perpendicular tanto al eje \(y\) como al eje \(z\).
  - El eje \(y\) es perpendicular tanto al eje \(x\) como al eje \(z\).
  - El eje \(z\) es perpendicular tanto al eje \(x\) como al eje \(y\).
  Sin embargo, ninguno de estos ejes (\(x, y, z\)) es paralelo a otro, ya que cada uno pertenece a planos diferentes (\(xy\), \(xz\), \(yz\)).
  

Y así sucesivamente.