Dilatación y contracción como transformaciones geométricas

La dilatación es una transformación geométrica que asocia a cada punto P(x;y) un nuevo punto P'(x';y') con coordenadas: $$ \begin{cases} x' = m \cdot x \\ \\ y' = n \cdot y \end{cases} $$ donde $ m,n \in \mathbb{R}^+ $ son dos números reales positivos.

Cuando m y n son mayores que 1, la figura experimenta una dilatación.

En cambio, si m y n toman valores entre 0 y 1, se produce una contracción.

Por tanto, la contracción puede interpretarse como la transformación inversa de la dilatación.

Si n = 1, se trata de una dilatación o contracción únicamente en dirección horizontal, según si m > 1 o 0 < m < 1.

Si m = 1, la transformación afecta solo al eje vertical, y será una dilatación o contracción según si n > 1 o 0 < n < 1.

En el caso de una función $ y = f(x) $, la dilatación puede expresarse así: $$ y = n \cdot f\left( \frac{x}{m} \right) $$

Un ejemplo práctico

Consideremos cuatro puntos en el plano cartesiano: A(2;2), B(4;2), C(4;4) y D(2;4), que corresponden a los vértices de un cuadrado.

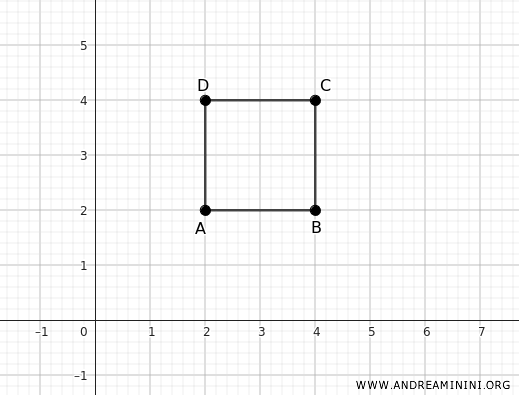
Aplicamos ahora una dilatación vertical con n = 2 y una dilatación horizontal con m = 3.

El punto $ A(2;2) $ se transforma en $ A'(4;6) $

$$ A' (2 \cdot n ; 2 \cdot m ) = A' (2 \cdot 2 ; 2 \cdot 3 ) = A' (4; 6 ) $$

El punto $ B(4;2) $ se transforma en $ B'(8;6) $

$$ B' (4 \cdot n ; 2 \cdot m ) = B' (4 \cdot 2 ; 2 \cdot 3 ) = B' (8; 6 ) $$

El punto $ C(4;4) $ se transforma en $ C'(8;12) $

$$ C' (4 \cdot n ; 4 \cdot m ) = C' (4 \cdot 2 ; 4 \cdot 3 ) = C' (8; 12 ) $$

El punto $ D(2;4) $ se transforma en $ D'(4;12) $

$$ D' (2 \cdot n ; 4 \cdot m ) = D' (2 \cdot 2 ; 4 \cdot 3 ) = D' (4; 12 ) $$

Tras la transformación, los puntos A', B', C' y D' delimitan un rectángulo.

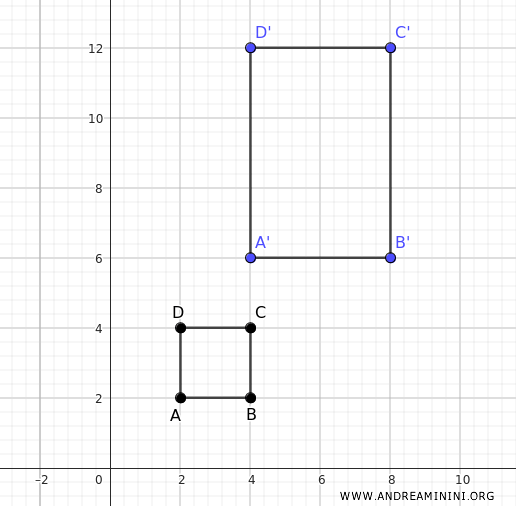
Ejemplo 2

Para comprender mejor cómo se aplica la dilatación a una función, analicemos la función cuadrática \( f(x) = x^2 \).

$$ f(x) = x^2 $$

El gráfico original de la función es el siguiente:

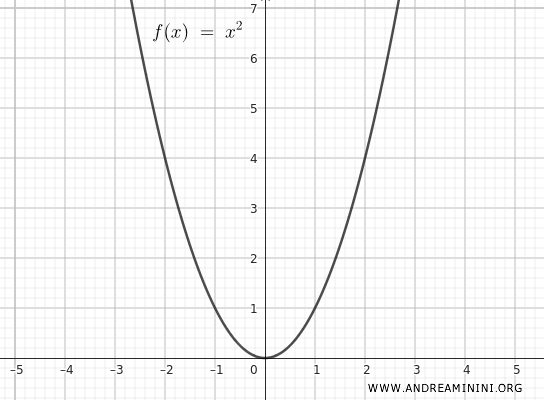
Veamos ahora cómo varía la función al aplicar dilataciones y contracciones, tanto verticales como horizontales.

Dilatación o contracción vertical

Para modificar la función verticalmente, se multiplica todo el valor de la función por un factor \( n \).

Si \( n > 1 \), la parábola se estira verticalmente; si \( 0 < n < 1 \), se comprime.

$$ y = n \cdot f(x) = n \cdot x^2 $$

Por ejemplo, si $ n = 3 $, se obtiene:

$$ y = 3x^2 $$

Esta transformación triplica el valor de \( f(x) \) en cada punto del dominio.

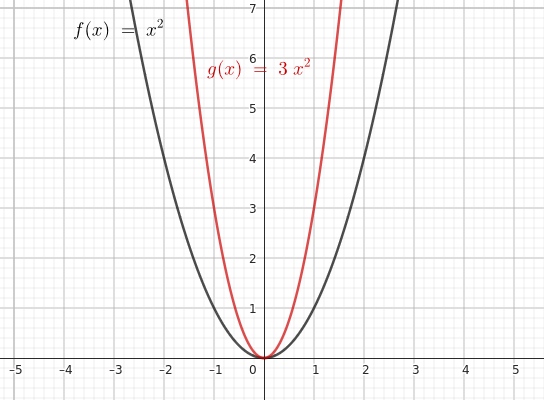
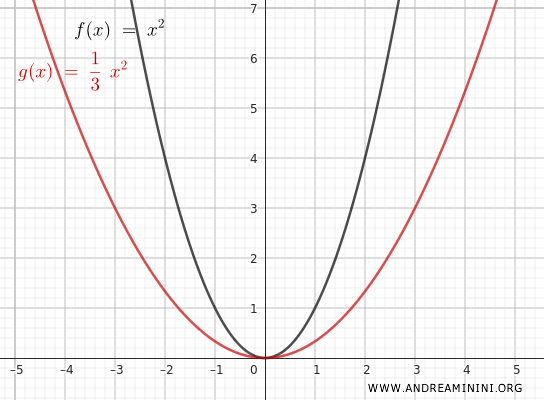
Si se aplica $ n = \frac{1}{3} $, la función se transforma en:

$$ y = \frac{1}{3} \cdot x^2 $$

En este caso, la función se contrae verticalmente.

Dilatación o contracción horizontal

Para modificar la función horizontalmente, se sustituye \( x \) por \( \frac{x}{m} \) dentro de la función.

Si \( m > 1 \), la parábola se ensancha en el eje x; si \( 0 < m < 1 \), se estrecha.

$$ y = f\left(\frac{x}{m}\right) = \left(\frac{x}{m}\right)^2 $$

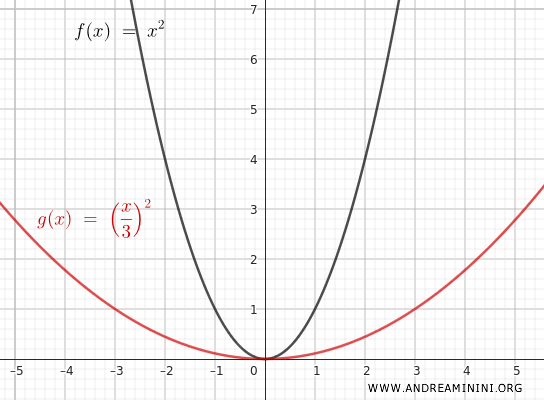
Por ejemplo, si \( m = 3 \):

$$ y = \left(\frac{x}{3}\right)^2 = \frac{x^2}{9} $$

La parábola se vuelve más ancha en dirección horizontal.

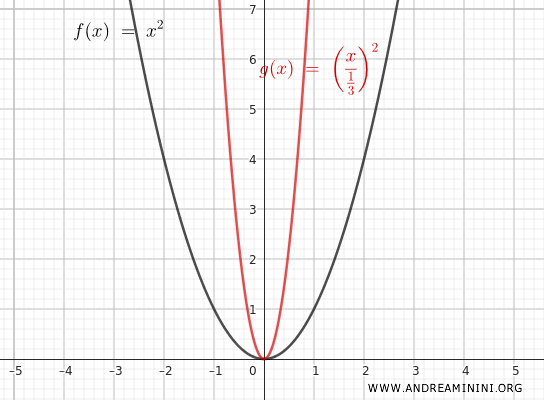
Si aplicamos $ m = \frac{1}{3} $, obtenemos:

$$ y = \left(\frac{x}{ \frac{1}{3} }\right)^2 = \frac{x^2}{\frac{1}{9}} = 9x^2 $$

En este caso, la parábola se comprime horizontalmente.

Dilatación o contracción combinada

También se pueden combinar ambas transformaciones: vertical y horizontal.

En ese caso, la función adopta la forma:

$$ y = n \cdot f\left(\frac{x}{m}\right) = n \cdot \left(\frac{x}{m}\right)^2 $$

Por ejemplo, si \( n = 3 \) y \( m = 2 \), la función transformada será:

$$ y = 3 \cdot \left(\frac{x}{2}\right)^2 = 3 \cdot \frac{x^2}{4} = \frac{3x^2}{4} $$

Esta transformación estira la parábola verticalmente por un factor de 3 y horizontalmente por un factor de 2.

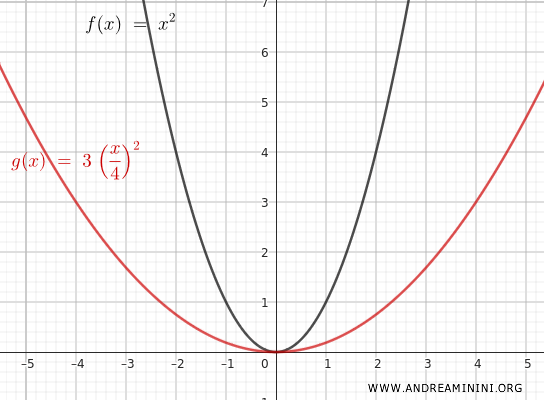
Por ejemplo, si \( x = 2 \), \( f(x) = 2^2 = 4 \) pasa a ser \( y = \frac{3 \cdot 4}{4} = 3 \); y si \( x = 4 \), \( f(x) = 16 \) se transforma en \( y = \frac{3 \cdot 16}{4} = 12 \).

En resumen, en la función cuadrática \( f(x) = x^2 \), las dilataciones y contracciones verticales y horizontales alteran la forma y la amplitud de la parábola.

Notas

Algunas observaciones complementarias y comentarios personales

• Las dilataciones dentro de las transformaciones afines
  Una dilatación es, en esencia, un caso específico de transformación afín, porque sus factores de escala \( m \) y \( n \) son ambos distintos de cero. Esto significa que la transformación conserva su carácter invertible y mantiene una estructura geométrica clara. En coordenadas, se expresa como: $$ \begin{cases} x' = m x + p \\[4pt] y' = n y + q \end{cases} $$ En esta forma, \( n \) controla la expansión o contracción a lo largo del eje \( x \), mientras que \( n \) regula el mismo efecto en la dirección del eje \( y \). Estos parámetros actúan como factores de escala direccionales que determinan cómo la figura original se deforma de manera distinta en cada eje, algo muy característico de las dilataciones en geometría afín.

  Observación. Dado que \( m \) y \( n \ne 0 \), el determinante de la parte lineal tampoco se anula. Esto asegura que la transformación sea un automorfismo afín del plano, es decir, una aplicación reversible que preserva la estructura afín: $$ \begin{vmatrix} m & 0 \\ 0 & n \end{vmatrix} = mn \ne 0 $$

Y así sucesivamente.