Relación entre el lado y la altura de un triángulo equilátero
Es posible determinar la longitud del lado de un triángulo equilátero si se conoce su altura, utilizando la siguiente fórmula: $$ l = \frac{2h}{ \sqrt{3} } $$
En ocasiones, esta misma relación se expresa de forma equivalente como:
$$ l = \frac{2 \cdot \sqrt{3} }{3} h $$
Ambas expresiones conducen exactamente al mismo resultado.
La fórmula inversa permite calcular la altura (h) de un triángulo equilátero cuando se conoce la longitud de su lado (l): $$ h = \frac{ \sqrt{3} }{2} l $$
Un ejemplo práctico
Veamos un ejemplo con un triángulo equilátero cuyo lado mide 3 unidades y cuya altura es \( h = 2.5981 \).
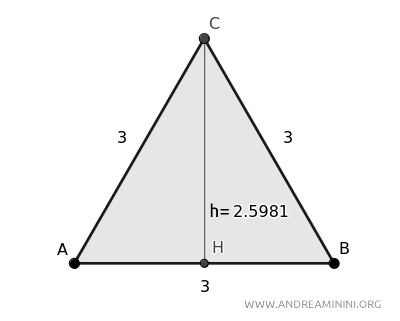
Utilizaremos la fórmula para verificar que se cumple la relación entre el lado y la altura.
$$ l = \frac{2h}{ \sqrt{3} } $$
Sustituyendo \( h = 2.5981 \), realizamos el cálculo para obtener la longitud del lado:
$$ l = \frac{2 \times 2.5981}{ \sqrt{3} } $$
$$ l = \frac{5.1962}{ \sqrt{3} } $$
$$ l = 3 $$
Esto confirma que la longitud del lado del triángulo equilátero es efectivamente de 3 unidades.
Demostración
Consideremos un triángulo equilátero.
Por definición, sus tres lados tienen la misma longitud \( l \):
$$ l = \overline{AB} = \overline{BC} = \overline{AC} $$
A continuación, trazamos la altura (h) desde el vértice superior hasta la base AB.
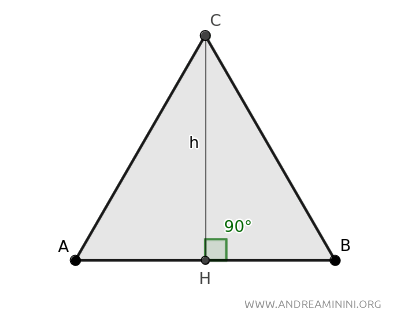
En un triángulo equilátero, la altura corta la base AB en ángulo recto y la divide exactamente en dos segmentos iguales, de modo que \( AH = BH \), siendo H el punto medio de AB.
Esta altura divide el triángulo equilátero en dos triángulos rectángulos congruentes.
En este punto, podemos aplicar el Teorema de Pitágoras para determinar la longitud del cateto HC en el triángulo rectángulo AHC:
$$ \overline{HC} = \sqrt{\overline{AC}^2 - \overline{AH}^2} $$
Identificamos el segmento HC como la altura \( h \), y el segmento AC como el lado \( l \) del triángulo ABC:
$$ h = \sqrt{l^2 - \overline{AH}^2} $$
Como el segmento AH es la mitad de la base AB (que mide \( l \)), podemos expresarlo como \( l/2 \):
$$ h = \sqrt{l^2 - \left( \frac{l}{2} \right)^2} $$
Simplificamos paso a paso:
$$ h = \sqrt{l^2 - \frac{l^2}{4} } $$
$$ h = \sqrt{\frac{4l^2 - l^2}{4} } $$
$$ h = \sqrt{\frac{3l^2}{4} } $$
$$ h = \frac{l}{2} \sqrt{3} $$
Así obtenemos la fórmula que nos permite calcular la altura a partir de la longitud del lado de un triángulo equilátero.
Para despejar \( l \) en función de \( h \), multiplicamos ambos lados de la ecuación por \( \frac{2}{\sqrt{3}} \):
$$ h \cdot \frac{2}{\sqrt{3}} = \frac{l}{2} \sqrt{3} \cdot \frac{2}{\sqrt{3}} $$
$$ \frac{2}{\sqrt{3}} h = l $$
Esto nos da la fórmula inversa para hallar la longitud del lado cuando se conoce la altura:
$$ l = \frac{2}{\sqrt{3}} h $$
Nota: En ocasiones, esta última fórmula se expresa en otra forma, dejando el radical en el numerador. Para conseguirlo, multiplicamos y dividimos el segundo miembro por \( \sqrt{3} \): $$ l = \frac{2}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} \times h $$ $$ l = \frac{2 \cdot \sqrt{3} }{\sqrt{3} \cdot \sqrt{3}} h $$ $$ l = \frac{2 \cdot \sqrt{3} }{3} h $$
Y así sucesivamente.